Op Art and More 

Die von Ralf Otte beschriebenen Iterationsverfahren auf Basis von Julia-Funktionen kann man als Näherung der Ausprägung von Sinus-Wellen und deren Abarten in einem komplexen Zahlenraum ansehen, die sich durch Überlagerungen, geeignete Störgrößen oder Redundanzen derart beeinflussen lassen sollten, dass Informationen im Sinne einer Wellenmodulation Bestandteil einer Basiswelle werden. Physikalisch sollten sich derartige Modulationen mittels elektromagnetischer Wellen beispielsweise durch Laserstrahlen realisieren lassen. Allerdings bezieht sich Ralf Otte nicht auf Wellen, die sich durch den einfachen komplexen mathematischen Zahlenkörper berechnen lassen, sondern auf einen hyperkomplexen Zahlenkörper mit einer speziellen Algebra, die in eine Richtung konkrete Spiegelungen in einem Beobachtungsfeld zulässt und in die andere Richtung Rückspiegelungen, die allerdings nur statistische Werte auf Basis von Wahrscheinlichkeitsdichten im Möglichkeitsfeld zulässt, die dann aber ihrerseits zur Auslösung veränderter oder neuer nicht-energetischer Wellen aus dem Möglichkeitsfeld führen können. Eine Beobachtung gespiegelter Wellen im Beobachtungsfeld setzt die Interaktion der Wellen mit Objekten voraus - beispielsweise beim Kollaps der Welle würde der korpuskulare Charakter des Photons durch Reaktion mit einem Elektron, das seinerseits vor dieser Reaktion ebenfalls einen Wellencharakter aufweist, sichtbar, indem durch Änderung des energetischen Levels des Elektrons ein Photon mit ebenfalls geänderter Energie wiederum in Wellenform auf einen Beobachtungsschirm trifft. Dort findet erneut ein Kollaps dieser nun veränderten Welle bei der Interaktion mit den gebundenen Elektronen des Beobachtungsschirms statt, die im Beobachtungsfeld im Bewusstsein des Menschen sichtbar werden können.

Wenn man derartige Prozesse zur Speicherung von Informationen im Möglichkeitsfeld nutzen will, dann macht es Sinn - wie von Ralf Otte vorgeschlagen - Verschränkungskorrelationen zu verwenden, bei denen ein nicht direkt beobachtbares Objekt im Möglichkeitsfeld über Fernwirkung mit einem korrelierten beobachtbaren Objekt im Beobachtungsfeld interagieren zu lassen. Als Objekt in Betracht kommt beispielsweise der Spin von Elektronen, der immer nur 2 verschiedene Zustände annehmen kann (Spin 1/2 oder -1/2). Bei Objekten dieser Größenordnung müssen allerdings die Effekte, die kurz im Abschnitt 6 ("Spiegelung") angesprochen wurden und die sich durch die Planck-Größen ergeben, genauer untersucht werden. Die Auswirkung derartiger Effekte sollte auch durch das mathematische Modell berücksichtigt werden.

Nicht zuletzt sollten auch die hinter diesen Effekten stehenden Bewusstseinsprozesse, die man als Ausstrahlungen des Möglichkeitsfeldes in das Beobachtungsfeld ansehen kann, betrachtet werden. Ralf Otte zeigt einige Interpretationsmöglichkeiten zu diesem Sachverhalt auf, wobei er zumeist davon ausgeht, dass wahrgenommene Objekte einen real existierenden Objektcharakter besitzen und das wahrnehmende Ich ebenfalls ein existentes Subjekt darstellt.

Aus Sicht mehrerer tib. Schulen - insbesondere dem Madhyamaka Nagarjunas - besteht allerdings keine reale Existenz von Objekten im Beobachtungsfeld und auch nicht im Möglichkeitsfeld. Danach bestehen Objekte nur dem Anschein nach! Das gilt auch für geistige Objekte/Phänomene, wie Gedanken, Emotionen, dem Selbst, dem Ich-Gefühl usw. Diese scheinbaren Objekte/Phänomene üben aber eine Wirkung aus, die zu Veränderungen zwischen diesen scheinbaren Objekten führen (z.B. körperliches Empfinden von Emotionen, wobei diese Empfindungen selbst keine Eigenexistenz besitzen, sondern wiederum nur dem Anschein nach entstehen). Nach Chögyam Trungpa kann man diese üblicherweise als Karma bezeichneten Auswirkungen, die man mit einer Kombination der herkömmlichen physikalischen Gesetze und dem statistisch zufälligen, aber gerichteten Wirken in einem nicht beobachtbaren, einen allenfalls indirekt ansatzweise interpretierbaren Raum (dem Dharmakaya, den man als Quantenvakuum verstehen könnte) ansehen kann. Daraus resultiert eine als inhaltlich äquivalente Beschreibung zu den Spiegelungen zwischen Möglichkeitsfeld und Beobachtungsfeld, die durch die hyperkomplexen Funktionen von Ralf Otte definiert wurden. Die von Ralf Otte beschriebene Spiegelung findet sich als Interpretation von James Low einer speziellen Verwirklichung von Wahrnehmungsaspekten auch in tibetischen Texten als unbedingter "Allgemeiner Natürlicher Zustand" (Möglichkeitsfeld) und als den Aspekt des Wissens um den "Eigenen Natürlichen Zustand" (Beobachtungsfeld) wieder.

Vor Betrachtung der dabei entstehenden Bewusstseinsprozesse zunächst aber ein Blick auf potenzielle Wirkungen der Mathematik bzw. der Algorithmen auf Iterationen bei gebrochenen Geometrien wie den Julia-Funktionen.

---

Der Raum der Gleitkommazahlen G

Die Menge der Gleitkommazahlen G in Verbindung mit ihren in Gleitkommaprozessoren angelegten Rechenregeln können nach Jürg Nievergelt bei entsprechenden linearen Rekursionsformeln mit bestimmten Parametern dazu führen, dass Rundungsfehler zu exponentiell wachsendem Rauschen führen, das ein chaotisches Verhalten mit einem Ergebnis produziert, das von der Darstellung Seltsamer Attraktoren nicht mehr zu unterscheiden ist. Die Menge G stellt eine Teilmenge des Raumes der reellen Zahlen ℝ und auch eine Teilmenge des Raumes der rationalen Zahlen ℚ dar. G ist eine beschränkte, abzählbare Menge, bei der bestimmte Rechenoperationen als Folge der Beschränktheit Ergebnisse produzieren, die eigentlich Bestandteil von ℝ sein müssten, die aber auf Ebene von G als Rundungsfehler mit einem Ergebnis wiederum aus G resultieren.

Jürg Nievergelt hat in seinen Beispielen dabei das Kreuzprodukt von G X iG durch algorithmische Abbildung des Kreuzprodukts auf die Teilmenge des Körpers ℂ angewandt (mit i als komplexer Zahl eines skalaren Produkts eines komplexen Vektorraums mit den Eigenschaften einer kommutativen Gruppe ohne die Unbegrenztheit reeller Zahlen). Diese Art der Berechnungen wurde auch bei den hier verwendeten Darstellungen von Julia-Funktionen verwendet. Im Abschnitt 3 "Hyperbolische Wellen" wurde bereits ein Beispiel mit einer oszillierenden Darstellung und fraktalen Substrukturen auf Basis der dort genannten Fuzzy-Abstände gezeigt. Diese Fuzzy-Abstände entsprechen keiner Metrik, da sie negative Werte enthalten können und somit eigentlich unzulässige Abstandswerte wiedergeben. Wenn man aber die Aussagen von Brian Greene betrachtet, denen zu Folge unterhalb der Planck-Länge auch Werte mit negativen Abständen auftreten können, dann macht es Sinn zu schauen, ob man die hier gewählten Fuzzy-Abstände als Modell für die Darstellung von Längen unterhalb der Planck-Länge verwenden kann. Diese künstliche "Planck-Länge" der hier verwendeten Gleitkommamenge G sollte sich aus der Beschränktheit von G und den Rechenregeln des Gleitkommaprozessors bzw. der hier verwendeten Java Virtual Machine (JVM) ermitteln lassen.

Im Folgenden wird daher zunächst noch einmal das Verhalten derjenigen Fuzzy-Abstände, deren Bildung durch Anwendung einer modifizierten Manhattan-Metrik gegen die allgemein gültigen Regeln einer Metrik verstoßen, genauer betrachtet. Die korrekte Anwendung einer Manhattan-Metrik führt zur Summation von Rasterlängen unabhängig von den eingeschlagenen 4 "Himmelsrichtungen". Die hier abgewandelte Form der Manhattan-Metrik wird dagegen durch Beibehaltung der Vorzeichen der 4 Himmelsrichtungen gebildet, wobei als Ergebnis in Abhängigkeit von den 4 Himmelsrichtungen auch negative Abstandswerte entstehen können. Die Himmelsrichtungen besitzen ein ähnliches Analogon in der Riemannschen Zahlenkugel für ℂ, die auf eine 2-dimensionale Ebene gelegt wird, wobei der Südpol mit der Repräsentanz von 0 auf der Ebene aufliegt und der Nordpol der Zahlenkugel mit seiner Repräsentation von ∞ in der 3. Dimension oberhalb vom Südpol liegt. Aus Sicht eines Betrachters sähe die Riemannsche Zahlenkugel dann aus wie auf dem Bild 3 des vorherigen Abschnitts, bei der die Realwerte der reellen Achse (in transparentem Grau) hervorgehoben wurden.

Die Fuzzy-Abstände entsprechen nun nicht der Riemannschen Zahlenkugel, sondern können in den Grafiken vielmehr als Repräsentanten von Resultierenden von je 2 Vektoren in der 3. Dimension angesehen werden. Zu jedem Pixel wird diese Resultierende nach den (modifizierten) Regeln der Manhattanmetrik gebildet, wobei die Darstellung in Analogie zur Zahlenkugel einer jeden Aufsicht auf jedes Pixel aus Richtung des "Nordpols" entspricht, wobei die Kugel mit ihrem Südpol jeweils auf jedes Pixel verschoben wird. Bei dieser Darstellung bleibt der Vektor punktförmig. Die Resultierende wird dann durch Farbwahl angezeigt, wobei negative Werte, die in eine Richtung unterhalb der Darstellungsebene weisen, von positiven Werten, die zum Nordpol weisen, farblich unterschiedlich dargestellt werden. Auf diese Weise werden Pixel mit gleicher Farbzuweisung als flächenförmige Gebiete vom Betrachter wahrgenommen.

Im Hinblick auf die Problematik der Gültigkeit von Cauchy-Folgen bezogen auf die Randbedingungen von G und den grundsätzlichen Beschränkungen durch die künstlichen Planck-Größen wird im Folgenden davon ausgegangen, dass zumindest bei Beschränkung auf Teilfolgen ohne Grenzwertbildung für das von der Julia-Fläche umschlossene Gebiet (Julia-Fläche) gilt, dass alle auf Pixelebene ermittelten konvergierenden Teilfolgen im Rahmen einer Unschärfe Cauchy-Folgen gleichgesetzt werden. Diese Gebiete würden dann im Rahmen einer gewissen Genauigkeit einem Banachraum gleichgesetzt.

Allerdings gibt es noch eine weitere Problematik bei der Verwendung von G: Wegen der Begrenztheit von G lassen sich nicht beliebige Vergrößerungen des Maßstabs der Koordinatenebene vornehmen. Hier gibt es eine (oder mehrere?) natürliche Grenzen, die man als Analogie zur physikalischen Planck-Länge ansehen kann. Bei einer Überschreitung einer maximalen Vergrößerung (also einer extremen Verkleinerung der Zahlengeraden des Koordinatenfensters) bricht der Bildaufbau ab, da dann der Gleitkommaprozessor und das endliche Zahlenformat von Gleitkommazahlen keine weiteren Rechenoperationen mehr zulassen und ein undefinierter Zustand entsteht.

---

Negative Abstände bei (z³ + c) / z

Bei der oben beschriebenen Art der Darstellung von resultierenden Vektoren als farbige Punktsymbole entstehen bei einigen Julia-Funktionen bei Verwendung einer passenden Störgröße c Flächenstrukturen im Sinne von Mengen, die ihrerseits fraktalen Charakter aufweisen. Handelt es sich dabei um "reale" Fraktale oder um chaotische Bildformationen, wie sie von Jürg Nievergelt und Peter Schorn gezeigt wurden? ( "real" hier in der Bedeutung der Sichtbarkeit einer Erscheinung, die einerseits nicht existiert, andererseits aber auch nicht nicht-existiert analog zur Betrachtungsweise im Madhyamaka, woraus sich aber auch ergibt, dass die duale aristotelische Logik sich als unzureichend herausstellt)

Um sich der Fragestellung einer möglichen Existenz der chaotischen Formationen als eigenständige Fraktale zu nähern, wird ein Beispiel mit Cauchy-(Teil)-Folgen auf Basis der Julia-Funktion (z³+c)/z näher betrachtet. Bei den Fuzzy-Abständen werden hier positive und negative Abstände durch schwarz/weiße Konturierung voneinander abgegrenzt, in Annäherung an die Signumfunktion.

Dazu werden mehrere Bildserien dargestellt, bei denen jeweils ein Bild mit Wahrscheinlichkeitsdichten einem Bild mit Fuzzy-Abständen gegenübergestellt wird. Alle Darstellungen der chaotischen Strukturen von Jürg Nievergelt weisen unscharfe Strukturen auf, die zudem noch auf verdichteten Punktewolken in Form disjunkter Mengen basieren (wegen fehlenden Copyrights können diese Bilder hier nicht angezeigt werden). Die hier gezeigten Bilder zeigen dagegen im Rahmen der Genauigkeit der Pixelgröße auf dem Bildschirm Strukturen, aus den sich direkt ein Rand und somit auch auf Pixelbasis begrenzte Mengen konstruieren lassen, was bei den Bildern von Jürg Nievergelt und Peter Schorn nicht der Fall ist. Allerdings zeigen sich bei einigen Bildern neben Strukturen, die einen Rand bilden können, in unmittelbarer Nachbarschaft auch Strukturen aus Einzelpixeln, aus denen sich kein Rand konstruieren lässt (siehe beispielsweise vergrößerte Darstellung von Serie 1 Bild 8), wenn man davon absieht, dass auch Einzelpixel gleichzeitig eine Fläche und einen Rand repräsentieren können. Diese Einzelpixel sind aber im Rahmen der Genauigkeit von Pixeln auch auf den Darstellungen der Wahrscheinlichkeitsdichten (Serie 1 Bild 7) erkennbar. Eine eindeutige Aussage über die Existenz fraktaler Substrukturen in den Julia-Flächen lässt sich auf diese Weise nicht treffen.

Serie 1: Einzelpixel als Punktewolke vs. Flächenobjekte

Detailbilder und tiefer gehende Iterationen (vergleiche Bilder 1-12) zeigen, dass der Effekt des Auftretens von Einzelpixeln, die auch bei den Bildern mit den dargestellten Wahrscheinlichkeitsdichten auftreten, erhalten bleibt.

---

Bei den Bildern 6 - 12 handelt es sich um Ausschnittsvergrößerungen; teilweise mit größeren Iterationstiefen.

---

Serie 2: Einfluss der Iterationstiefe

In der Bilderserie 2 wird exemplarisch dargestellt, zu welchen Auswirkungen der Iterationsprozess von 40 bis 4000 bei den Fuzzy-Werten führt (Bild 2-4 in Serie 2). Hier werden keine Wahrscheinlichkeitsdichten dargestellt, da dann fast ausschließlich schwarze Flächen, die einen niedrigen Wahrscheinlichkeitswert widerspiegeln, zu sehen sind. Bild 1 zeigt ein Übersichtsbild. Die Vergrößerung in den Bildern 2-4 bleibt konstant, so dass sich die Effekte besser vergleichen lassen. Gegenübergestellt werden Bilder mit einer etwas höheren Vergrößerung und unterschiedlichen Iterationstiefen (Bilder 5-7).

Bei den Bildern 2-4 wurde der Zentralbereich aus Bild 1 vergrößert. Das Koordinatenfenster dieser 3 Bilder wurde konstant gehalten.

Bei genauerer Betrachtung der höher aufgelösten Bilder kann man feststellen (insbesondere bei Bild 3 und 4), dass kleine farbige kreisförmige Strukturen sichtbar werden. Hierbei handelt es sich mathematisch gesehen um Löcher in der von der Julia-Menge umgebenen Fläche, so dass es in einem mehrfach zusammenhängenden Raum Wege gibt, die nicht durch stetige Deformation ineinander überführt werden können.

Bei Bild 4 wird außerdem sichtbar, wie oszillierende Strukturen bereits in kleinsten Formationen auftreten können. Im Video, das in Abschnitt 3 ("Hyperbolische Wellen") gezeigt wird, lassen sich die Effekte der groß- und kleinräumigen Oszillationen als Bewegtbilder besser erkennen. Auch wird in den Schlussbildern des Videos die Beziehung zwischen Loch und zu der von der Julia-Menge umgebenen Flächen (Julia-Flächen) klarer sichtbar.

In den Bildern zeigt sich auch, dass sich bei zunehmender Iterationstiefe flächige Gebiete zunehmend auflösen. In Bild 4 überwiegen kleine und sehr kleine Strukturen, die optisch den Punktwolken bei Jürg Nievergelt ähneln. Gegenüber Bild 2 sieht man außerdem eine geringfügige Zunahme von Löchern als kleine Farbpunkte umgeben von runden flächigen Objekten mit der Signatur positiver bzw. negativer Fuzzy-Abstände.

Eine sichere Folgerung, ob die Darstellung das Resultat chaotischen Verhaltens der Gleitkommarechnung ist, lässt sich aber nicht treffen.

Aus den Bildern resultiert aber die Frage, ob erhöhte Iterationsschritte zu einem Lückenschluss bei schwarzen bzw. weißen Teilflächen führen. Die Bilder 5-7 zeigen, wie sich Lücken dem Anschein nach zunehmend schließen, aber auch wie bei Bild 7 flächige Objekte als Teilmenge der Julia-Fläche zunehmend zerfallen. Hieraus lässt sich folgern, dass die flächigen Objekte nur dem Anschein nach bestehen, also im Sinn der Philosophie des Madhyamaka als leer gelten - d.h. also nur dem Anschein nach existieren.

---

Serie 3: Wechsel positiver und negativer Fuzzy-Werte

Um eine bessere Einschätzung zu den Formationen bei den Fuzzy-Abständen und ihrer Realität bzw. Fiktivität zu erhalten, werden im Folgenden die berechneten Zahlenwerte zwischen positiven und negativen Abständen verglichen und auch den Wahrscheinlichkeitsdichten gegenübergestellt. Dazu wird ein Bereich ausgewählt, bei dem sich der Übergang gut verfolgen lässt. Verwendet wird wieder die Julia-Funktion (z³+c)/z, mit einer Ausschnittsvergrößerung in einem Gebiet, bei dem zur besseren Vergleichbarkeit nur wenige Veränderungen vorkommen.

Bild 1 zeigt das Übersichtsbild. Ausgehend von diesem Übersichtsbild wird ein kleiner Teilausschnitt mit einem abrupten Übergang zwischen positiven und negativen Fuzzy-Abständen vergrößert (Bild 2). Von diesem Teilausschnitt werden für eine horizontale Linie für die 500 auf dem Bild vorhandenen Pixel die Fuzzy-Abstände und Wahrscheinlichkeitsdichten als Zahlenwerte ausgegeben. In Bild 2 ist diese horizontale Linie mit ihren Abstandsmarkierungen in 10er und 50er Schritten schwach zu erkennen. Die unten stehende Auflistung zeigt die Werte zwischen Pixel 408 und 418.

Die Grenze zwischen positiven und negativen Fuzzy-Abständen zeigt sich hier deutlich zwischen Pixel 413 und 414. Eine Grenzwertbildung als Limes einer Teil-Cauchy-Folge lässt sich zwischen diesen beiden Pixeln mit den hier vorgenommenen Einstellungen nicht erkennen. Die Zahlenwerte liegen aber wohl nahe bei 0. Aus den Wahrscheinlichkeitsdichten mit ihren extrem kleinen Werten lassen sich keine Besonderheiten erkennen. Daher wird im Folgenden eine weitere Auswertung in einem Gebiet durchgeführt, das optisch einer von Jürg Nievergelt beschriebenen Struktur entspricht.

---

Serie 4: Chaotische Strukturen

Bild 4 aus Serie 2 zeigt einen chaotischen Bereich teilweise vergleichbar einer Punktewolke, wie sie auch von Jürg Nievergelt als Folge von iterativen Rundungsfehlern bei Verwendung von Gleitkommazahlen beschrieben wurde. Aus dem Übersichtsbild 1 aus Serie 4 wurden nun aus dem Zentralgebiet Vergrößerungen mit 500 Iterationen vorgenommen, die ebenfalls einer Punktewolke ähneln, und deren Werte auch als Teilauszug hier dargestellt werden.

Bild 1 zeigt die Wahrscheinlichkeitsdichte in dem vergrößerten Bereich. Es enthält wenige kleine Löcher (Gebiete mit Wahrscheinlichkeitsdichten >4). Dargestellt hier und auch den weiteren Bildern dieser Serie ist auch der horizontale Pixelmaßstab basierend auf 500 Pixeleinheiten. In den Detailbildern, die auf der Berechnung von 1000 Pixeln beruhen, wird zur besseren Vergleichbarkeit bei der bildhaften Darstellung weiterhin der Maßstab von 500 Pixeleinheiten beibehalten.

In Bild 2 wurde dieselbe Ausschnittsvergrößerung mit der Darstellung der Fuzzy-Abstände gekennzeichnet in schwarz (negativ) bzw. weiß (positiv) gewählt. Im vergrößerten Bild ist auch der horizontale Pixel-Maßstab dargestellt, der wegen der vielen unterschiedlichen Strukturen aber nur schwer zu erkennen ist. Für diesen Ausschnitt wird unten ein Auszug mit den dort vorliegenden Ergebnissen angezeigt. Da in diesen Ergebnissen einige ungewöhnliche Einzelwerte auftreten, wurde weiter unten noch eine weitere Vergrößerung (Bild 3) vorgenommen, die in Bild 2 als rotes Rechteck angedeutet ist.

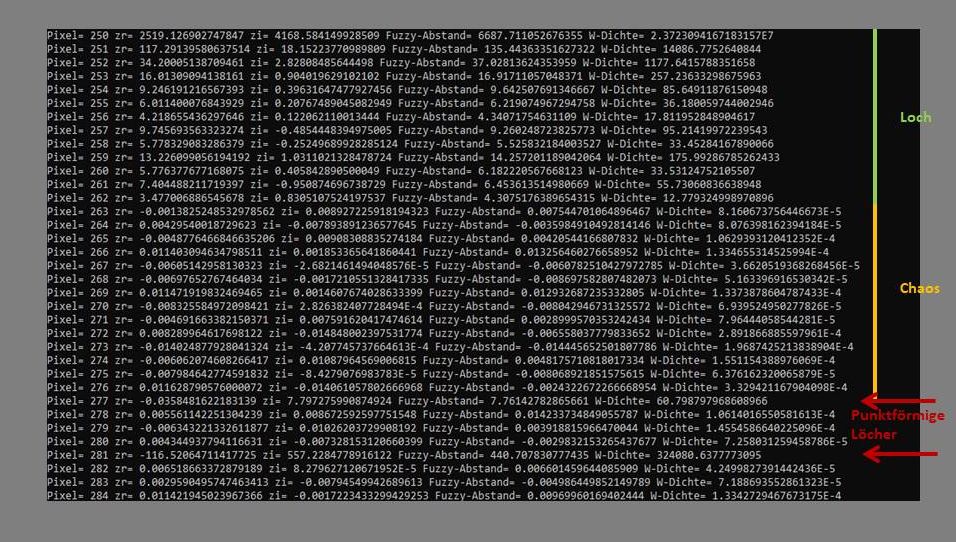
Zwischen den Pixeln 250 (Zentrum von Bild 2) und Pixel 262 lassen sich die Werte des Loches erkennen, bei denen höhere Fuzzy-Abstandswerte zu erkennen sind. Ungewöhnlich hoch ist aber auch die Wahrscheinlichkeitsdichte bei Pixel 250. Hier kann nur vermutet werden, dass der hyperbolische Term in (z³+c)/z die Ursache für einen derart hohen Wert ist. Nach dem Loch ab Pixel 263 treten - wie zu erwarten - abwechselnd positive und negative Fuzzy-Abstände auf, die auch die granulare Struktur in Bild 2 widerspiegeln; die Wahrscheinlichkeitsdichten besitzen hier wieder normale Werte knapp über 0. Ungewöhnlich sind aber die Werte bei Pixel 277 und 281. Es entsteht der Eindruck von kleinen Löchern, die aus nur 1 Pixel bestehen.

Um zu klären, worum es sich hier handelt, wurde in Bild 3 das Gebiet um diese beiden Pixel weiter erheblich auf 75.378 vergrößert. Im Zentrum von Bild 3 zeigt sich jetzt ein in diesem Maßstab deutlich erkennbares Loch. Der Auszug aus der Ergebnisliste beginnt erneut bei dem neu zentrierten Loch wiederum bei Pixel 250 und zeigt bis Pixel 258 wieder die typischen Daten eines Loches sowie anschließend wiederum die Werte der granularen Struktur.

Bei Bild 4 wurde der Bereich von Bild 3, in dem sich in den Daten 2 kleine Löcher verbergen (rotes Rechteck), erneut vergrößert, jetzt auf 6.207.053. Bei dieser Vergrößerung werden deutlich 2 weitere Löcher sichtbar. Die Bildstrukturen bei den verschiedenen Vergrößerungen erscheinen selbst-ähnlich, so dass zu erwarten ist, dass weitere Löcher in dieser Julia-Fläche vorhanden sind. Hieraus ergibt sich auch wiederum erneut die Frage, ob bei hinreichender Vergrößerung kombiniert mit hinreichender Iterationstiefe nicht an allen Koordinaten der Julia-Fläche dieser hyperbolischen Wellenfunktion Löcher auftreten und sich die Julia-Fläche somit insgesamt als leer bzw. nicht wirklich vorhanden herausstellt (sowohl im Sinne der Philosophie des Madhyamaka, als auch bei herkömmlicher Betrachtungsweise).

---

Negative Abstände bei der sinusförmigen Julia-Funktion z²+c

Im ersten Abschnitt dieses Essays wurde bereits ein Beispiel gezeigt, aus dem hervorgeht, dass die Zunahme der Iterationstiefe das Verschwinden von Julia-Flächen mit Wahrscheinlichkeitsdichten <4 bewirken kann, so dass Cauchy-Folgen anscheinend im Rauschen aufhören zu existieren. Aus diesem Grund werden im Folgenden Fuzzy-Abstände und Wahrscheinlichkeitsdichten bei dieser Julia-Funktion in einem alternierenden Bereich betrachtet. Dazu wird noch einmal die Julia-Funktion mit der Störgröße (-1.35, 0i) herangezogen, die bereits auf der vorherigen Seite "Simulation" verwendet wurde.

Serie 5: Stetigkeit?

Da höher iterierte Berechnungen häufig schnell zu Ergebnissen führen, bei denen es keine oder nur wenige beobachtbare Daten in Bezug auf die Wahrscheinlichkeit einer möglichen Beobachtung gibt, wurde hier bei vielen Betrachtungen nur eine kleine Zahl von Iterationen verwendet. Zu vermuten ist, dass auch bei geistigen Prozessen die Zeit bis zu einer Dekohärenz gering sein könnte (siehe hier auch Abschnitt 9 "Bewusstwerdung". Schließlich wurde durch meditative Untersuchungen von Geistprozessen festgestellt, dass für den kürzesten Prozess einer Bewusstwerdung 17 Schwingungen ausreichen (siehe hierzu die von Lama Anagarika Govinda beschriebenen Ergebnisse, die er aus den Aufzeichnungen von Bhadantácariya Buddhaghosa (5. Jahrhundert) abgeleitet hat. Ob diese Anzahl von Schwingungen mit der Anzahl von Iterationen übereinstimmt oder wie Iterationen und geistige Schwingungen korreliert sind, bleibt dahingestellt.

Die Beschränkung der Anzahl von Iterationen auf 17 ergeben allerdings Berechnungsergebnisse mit einem größeren zusammenhängenden Gebiet mit Wahrscheinlichkeitsdichten >4 und gleichzeitig einer geringeren Zahl von Löchern. Denkbar wäre, dass hieraus bei der rekursiven Selektion von Folgeprozessen eine höhere Wahrscheinlichkeit für stabile nachfolgende Prozesse mit Wahrscheinlichkeitswerten >0 resultieren. Im Abschnitt 8 "Attraktoren und Entscheidungsfreiheit" und Abschnitt 9 "Bewusstwerdung" wird gezeigt, wie derartige Prozessfolgen aussehen könnten und wie Schwarmintelligenz zu einer vorrangigen Auswahl von Folgeprozessen führen könnte, die zwar auf Wahrscheinlichkeiten beruht, aber deren Auswahl zusätzlich durch inhärente Schwarmregeln beeinflusst wird. Dieser Selektionsvorgang könnte identisch mit dem von Ralf Otte beschriebenen Prozess der Selbstreferenzen im Evolutionsprozess entsprechen; dies wäre aber noch zu überprüfen. Auch mögliche Auswirkungen auf die Philosophien wie dem Dzogchen und möglichen Diskrepanzen gegenüber Ralf Ottes Hypothese zur Evolution von Geist wäre noch zu untersuchen. Es soll an dieser Stelle nur kurz vermerkt sein, durch tiefergehende Geistexperimente die zwei Körper Dharmakaya (Möglichkeitsfeld) und Rupakaya/Formkaya (Kombination von virtuellem Beobachtungsfeld und Transformationsfunktion) in einen einzigen Körper (Svabhavikakaya) überführt werden können, den sogenannten Weisheitskörper auch Buddhakörper genannt. Aus diesem Svabhavikakaya heraus, in dem alle Prozesse in einem Körper zusammenfallen, kann nun ein selbstorganisiertes Handeln sichtbar werden, bei dem Bewusstheit für absolutes Wirken besteht und aber auch relatives Handeln zusammen mit Bewusstsein verbundenem Denken als relative Wahrheit aktiv sein können.

Herbert Guenther interpretiert Texte Padmasambhavas mit seiner spyi-ti-Lehre dahingehend, dass für die geistige Entwicklung die Wahrnehmung von Phasenräumen, die durch Symmetriebrüche getrennt sind, erkannt/erfahren/gefühlt werden muss. Hieraus ergibt sich ein Prozesscharakter des Geistig-Materiellen, der ausgehend von einem Zentrum/einer Nullpunkt-Energie nach Erreichen einer zeitlosen Grenzenlosigkeit, ohne aber das Begrenzte zu verlieren, erneut eine weitere Schleife bei der Nullpunkt-Energie fortgeführt wird. Dieser Prozess basiert ausgehend von einer Form des Gewahrseins/Bewusstheit auf der geistigen Entwicklung von 5 sogenannten Weisheiten, die über 5 weitere Spiegelungen zu einem höherwertigen Bewusstseinsprozess führen. Dieses höherwertige Bewusstsein kann zwischen nicht bewussten non-intellektuellen, non-analytischen Gedankenformen (Kette der 1. Nen) (des Möglichkeitsfeldes/des Dharmakaya) und analytisch-intellektuellen Gedanken gezielt wechseln. Diese Form der Bewusstheit könnte man mit einer Sicht aus einer Vogelperspektive auf das Geschehen am Erdboden vergleichen, wobei aber kein Ich vorhanden ist, das sieht, sondern lediglich eine nicht beschreibbare Bewusstheit, die das Verhalten eines illusionären Ich erkennt, das wiederum versucht, mittels Intellekt die Welt zu verstehen. James Low beschreibt diese Form der Bewusstheit wie folgt:

Bewusstheit bedeutet nicht, dass "Ich" mir einer Sache bewusst bin. Es ist nicht so, dass ich mir der Dinge bewusst bin, sondern es ist so, dass im Zustand von Bewusstheit das Empfinden eines "Ich" erscheint, welches anderen Erscheinungen innerhalb des Feldes der Manifestation Beachtung und Interesse schenkt.

Dieser geistige Entwicklungsprozess wird zumindest für die Dauer des Menschseins (das Sein, das Seiende des Seins, Sein an sich) immer wieder durchlaufen, sofern diese Energiemuster (dkyil-'khor) erkannt werden, was aber nur sehr wenigen Menschen möglich ist. Aus diesem Vorhandensein ergibt sich eine von Ralf Otte bestrittene höherwertige Form einer beim Menschen erfahrbaren Bewusstheit, deren Basis der Dharmakaya/das Möglichkeitsfeld ist und die auf einem Rückkopplungsprozess beruht. Hieraus ergeben sich zahlreiche Konsequenzen, die mit den Aussagen Ralf Ottes abzugleichen wären, was aber an dieser Stelle zu weit führt. Daher zunächst die weitere Betrachtung der Eigenheiten von Julia-Funktionen.

In Bild 1 werden die Werte der Fuzzy-Abstände als variierende bläuliche Farben (von weiß bis blau) dargestellt, wobei sich nur geringfügige Varianzen in den Julia-Flächen zeigen. Die Darstellung der Wahrscheinlichkeitsdichten des Übersichtbildes auf der vorherigen Seite zeigt hier größere Unterschiede.

Die Vergrößerung eines Teilbildes auf der linken Seite vom genannten Übersichtsbild (Bild 1) zeigt diese Unterschiede detailreicher (Bild 2).

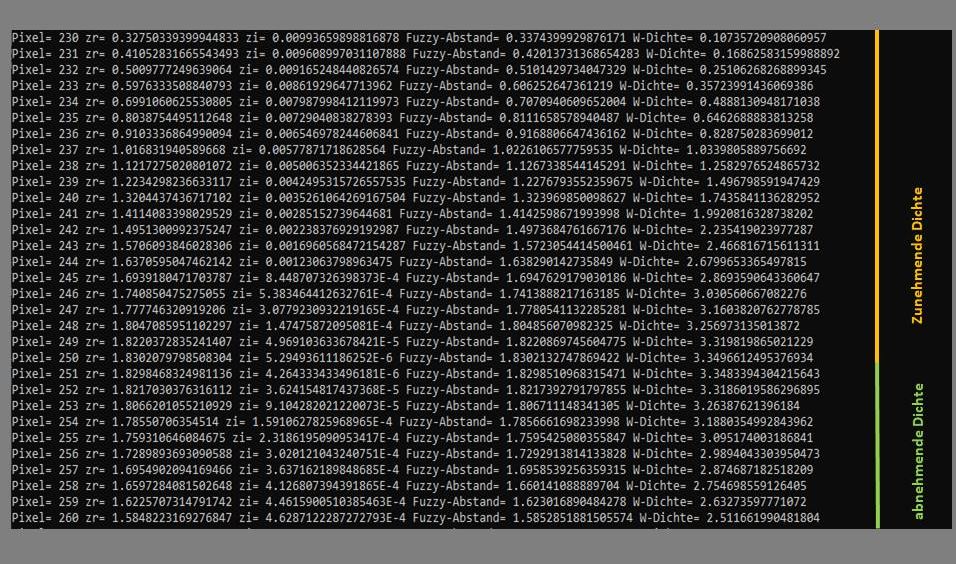
Die Auflistung enthält die Ergebnisse der Fuzzy-Abstände und die Werte der Wahrscheinlichkeitsdichten aus dem zentralen Bereich von Bild 2 von Pixel 230 - 260. Der Übergang der Wahrscheinlichkeitsdichten von niedrigen Werten zu höheren zeigt sich zwischen Pixel 250 und 251. Auch wenn sich hier ein scheinbar stetiger Verlauf zeigt, ist aber nicht sichergestellt, dass die unendlich vielen Koordinaten aus ℂ zwischen diesen beiden Pixeln bei hinreichend tiefer Iteration weiterhin immer zu stetig erscheinenden Werten führen, solange kein Nachweis über die Existenz zur Grenzwertbildung von Cauchy-Folgen bei Fraktalen erbracht werden kann.

Bei den hyperbolischen Wellengleichungen wird wohl durch den hyperbolischen Term in den Funktionsgleichungen die hohe Varianz und das Auftreten von Löchern hervorgerufen, die innerhalb der Julia-Flächen auch bei niedrigen Iterationstiefen zwar zu (scheinbar) zusammenhängenden Räumen führen aber mit Wegen zwischen fiktiven Punkten in den Räumen, die nicht durch Deformationen ineinander überführt werden können - also Löcher im Raum.

Bei der Julia-Funktion z²+c ist der Komplexitätsgrad des Raumes in ℂ dagegen erheblich geringer. Bild 3 zeigt eine Vergrößerung des Zentralbereichs von Bild 2 bei einer Iterationstiefe von 1001. Eine sichere Aussage, ob die Julia-Fläche zusammenhängend ist oder ob es sich um offene Teilmengen eines metrischen Raumes in ℂ handelt, lässt sich durch die Grafiken oder die Ergebnisse der Berechnungen nicht erschließen.

---

Fazit

Ralf Otte hat die von ihm konzipierten Beobachtungsfelder als virtuell charakterisiert, derart dass Veränderungen in der nicht-energetischen Wahrscheinlichkeitswelle des Möglichkeitsfeldes über die Transformationsfunktion zu Veränderungen der virtuellen Beobachterwelle führen, während umgekehrt Veränderungen im Beobachterfeld über Verschränkungskorrelationen die Wahrscheinlichkeitsamplituden der nicht-energetischen Wahrscheinlichkeitswelle rein statistisch ohne das Prinzip von Ursache und Wirkung und ohne Vorhersagbarkeit beeinflusst werden können. Hieraus lässt sich die Leerheit der virtuellen Spiegelfelder folgern, wie sie sich oben als Ergebnis des vermutlich unbeschränkten Auftretens von Löchern und dem augenscheinlichen Verschwinden konvergierender Cauchy-Folgen anscheinend ebenfalls zeigt.

Zu einer ganz ähnlichen Aussage kam im 2. Jahrhundert der indische Philosoph Nagarjuna durch Introspektion des Geistes mittels Meditationstechniken, aus deren Einsichten er seine Philosophie Madhyamaka ("Mittlerer Weg") entwickelte und schriftlich niederlegte. Nagarjuna hat für die Durchführung von Geistexperimenten für andere Meditierende in seinem Werk Dharmadhatustava (beschrieben von Karl Brunnhölzl) ein Konstrukt von 3 ineinandergreifenden "Körpern" (Kayas) mit dezidierten Eigenschaften erstellt, das den Meditierenden erlaubt, Nagarjunas eigene Geistexperimente in einem Erscheinungsraum (Dharmadhatu genannt) nachzuvollziehen. Die 3 Kayas (Dharmakaya, Sambhogakaya, Nirmanakaya) entsprechen inhaltlich weitgehend den von Ralf Otte definierten Möglichkeitsfeldern, der Transformationsfunktion und den virtuellen Beobachtungsfeldern. Hierbei können von Meditierenden konkrete und sehr klare, aber subjektive Bewusstseinserfahrungen auf den Ebenen ("Körpern") von Sambhogakaya und Nirmanakaya erfahren werden, während die Objektivität des Dharmakaya nicht beobachtbar ist, sondern allenfalls gefühlt werden kann.

Eine der grundlegenden Erkenntnisse Nagarjunas lautet in Form eines Aphorismus: "Alles existiert nur dem Anschein nach!". Der philosophische Nachweis für die sich daraus ergebende Leerheit aller Phänomene wird von Nagarjuna mittels Tetralogik vorgenommen. Nagarjuna beschreibt 20 verschiedene Arten des Leerseins, aus denen sich Folgerungen für verschiedene Erfahrungen ergeben; beispielsweise für das Untersuchen von Zeit oder Bewegung im Raum. Neben der von ihm angewandten Tetralogik führt Nagarjuna bisweilen auch eine Art logischer Cauchy-Folgen auf, bei denen er eine geistige Grenzwertbildung in Richtung beliebig kleiner Einheiten vornimmt und daraus Schlussfolgerungen zieht. Aus seiner Philosophie ergibt sich auch das Nicht-Vorhandensein von Unendlichkeitsaspekten bzw. jeglicher Form von Theismus, aber umgekehrt auch das Nichtvorhandensein eines Nihilismus, da auch das Leersein der Phänomene dazu führen kann, dass die Phänomene emotional wirksam sind und auf diese Weise zu Veränderungen von Zuständen des scheinbaren Körpers führen (z.B. durch Ausschüttung von scheinbaren Botenstoffen, die den scheinbaren Körper verändern und auch den Zustand des Geistes verändern). Hiermit beschreibt Nagarjuna ein ganz ähnliches Prinzip einer Übertragung von Informationen wie Ralf Otte mit der Speicherung von Informationen in einer virtuellen hyperkomplexen Spiegelwelle nach Multiplikation mit einer nicht-energetischen komplexen Wahrscheinlichkeitswelle des Wahrscheinlichkeitsfeldes. Spezielles meditatives Erleben des Nicht-Dualen, bei denen Subjekt und Objekt zu nicht-beschreibbarem "«Nicht»" (ohne "s" am Ende von Nicht) bzw. nicht beschreibbarem "«Nein»", von dem kein niemand und kein jemand sagen kann "dies ist es", verschmelzen, entspräche dann der von Ralf Otte beschriebenen Verschränkungskorrelation, die zu einer nicht vorhersehbaren Veränderung des Möglichkeitsfeldes führt.

Die Aussagen Nagarjunas, die im 7. Jahrhundert durch den indischen Philosophen Chandrakirti kommentiert wurden, sind mit ihrer holistischen Sicht insbesondere für den westlichen Kulturkreis teilweise schwer verständlich. Daher hat im Jahr 2000 Khenpo Tsultrim Gyamtso Rinpoche die Philosophie Nagarjunas einem westlichen Publikum mündlich erläutert. Diese Erläuterungen wurden von Christoph Klonk als Text aufbereitet (Taghelle Weisheit - Erforschung der Wirklichkeit), so dass sie jetzt für den westlichen Kulturkreis besser verständlich sind. Da aber das holistische Gedankengut und die Anwendung der Tetralogik in Verbindung mit der Wahrnehmung von Phänomenen in der eigenen Lebenserfahrung immer noch schwer nachzuvollziehen sind, wurden in einigen Städten (Bielefeld, Marburg, München, Wien, Köln) Studiengruppen unter der Leitung von Chriostoph Klonk eingerichtet, in denen der Text weiter erläutert wird, so dass die Aussagen Nagarjunas erfahrbar werden können.

---