In seiner Monographie "Vorschlag einer Systemtheorie des Geistes", Cuvillier-Verlag Göttingen (2016) beschreibt Prof. Ralf Otte unter anderem das unterschiedliche Verhalten
der Endzustände bei der Berechnung von Julia-Funktionen, die er als dynamisches, selbstorganisierendes Modell für Wahrnehmungs- und Bewusstwerdungsprozesse nutzt.
Da in diesem Essay hier Schwarmverhalten von Gedankenprozessen postuliert wird, wird im Folgenden versucht, Ansatzpunkte
für ein mögliches Schwarmverhalten zu finden.
Die Grafiken und Videos sind 2024 entstanden soweit nicht anders erwähnt
Das von Ralf Otte definierte Modell der Bewusstwerdung, das ebenfalls auf einem dynamischen, selbstorganisierenden
Iterierten Funktionensystem aufbaut,
steht bisher nicht im Widerspruch zu dem schon mehrfach genannten Schwingungsprozess, der von Lama Anagarika
Govinda beschrieben wurde, und auch nicht zu dem Modell über den Gedankenprozess der Drei Nen von
Katsuki Sekida, weswegen das
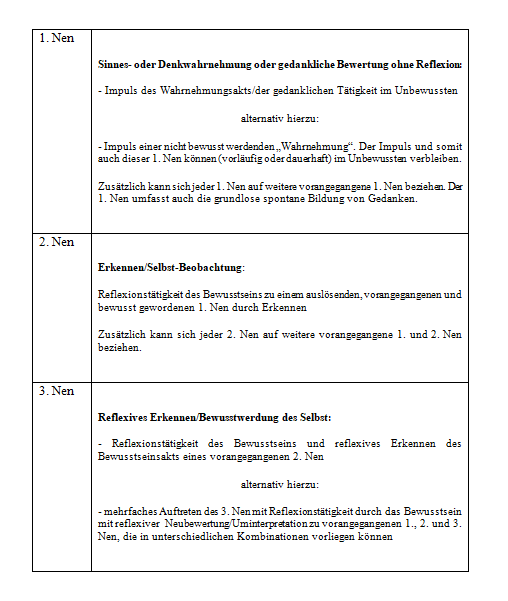
Modell der Drei Nen zunächst kurz beschrieben wird, dessen Schwerpunkt auf der Modellierung des Gedankenpozesses liegt. Die 3-stufige Struktur
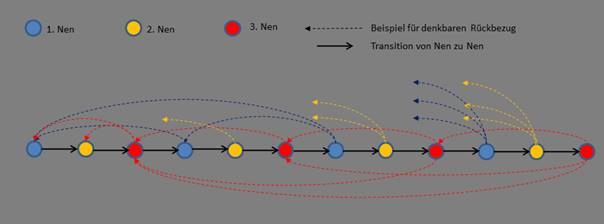
der Drei Nen zeigt Ähnlichkeiten mit dem ebenfalls 3-stufigen Modell von Ralf Otte mit Möglichkeitsfeld,
Transformationsfunktion und Beobachtungsfeld, wobei aber das Modell der Drei Nen nicht auf iterativen
Berechnungen beruht, sondern auf Rückbezügen zu vergangenen Nen, aus denen jeweils ein nächster Nen mit einer der 3 Charakteristiken hervorgeht (siehe folgende Tabelle).
Dieses Modell der Drei Nen entspricht im weitesten Sinne einem fortlaufenden, rekursiven Zustandssystem, bei dem permanent neue rückbezügliche Zustände mit 3
unterschiedlichen Qualitäten gebildet und vernetzt werden. Das endlos weiter laufende Zustandssystem entspricht dabei dem Graph einer endlosen fortlaufenden Baumstruktur mit
rückbezüglichen Verbindungen, wobei jeder neue Zustandsknoten dem gerade in diesem Moment entstehenden Bewusstseinsmoment bzw. Wahrnehmungsmoment entspricht.
Die folgende Aufstellung beschreibt in Kurzform die verschiedenen Typen der Drei Nen sowie ihre möglichen Beziehungen untereinander als verbales Prozessmodell:
(Die Grafiken zu den Drei Nen wurden übernommen aus
Gedanken über Gedanken - Teil III ) , 2020
Mit dieser Struktur sollte sich grundsätzlich auf Basis eines iterierten Vorgehens eine neue Stufe der Selbsterkenntnis
in einer höheren Ordnung als
die normalerweise erfahrbaren, verschiedenen Bewusstseinsformen (inkl. Ich-Gefühl mit reflexiver Selbsterkenntnis und Bewusstwerdung des Selbst)
bilden können. Die Struktur und die Rückbezüge der 3 Nen sollten daher grundsätzlich eine Möglichkeit zulassen, durch Selbstreferenz neue geistige
Eigenschaften zu entwickeln, die zu einem höheren geistigen Zustand führen, zumal sich die Drei Nen mit dem mathematisch rekursiven Prozessmodell von Ralf Otte
verknüpfen lassen. Dieses Modell entspricht nach Ralf Otte einem algorithmischen System, das in Anerkennung des Gödelschen Unvollständigkeitssatzes
die Erzeugung neuer Eigenschaften zulässt, die das ursprüngliche System übersteigen.
In einem (geplanten) Anhang II wird diese auch vom heutigen Menschen erfahrbare höhere, aber weitgehend unbekannte Form einer Bewusstheit,
wie sie in einigen buddhistischen Schulen praktiziert wird, weiter erläutert. In Anhang I wird gezeigt,
wie mit der Realisierung einer Kette des 1. Nen mit ihrer Form des "Denkens-ohne-zu-denken" eine Voraussetzung geschaffen werden kann,
eine höhere Form von Bewusstheit zu entwickeln.
Aus Übersetzungen von Texten Padmasambhavas durch Herbert Guenther kann man schließen, dass die Vorgänge des Zuhörens, Mitteilens und Verstehens mit einer
energetischen, ontologischen Prozessstruktur gleichgesetzt werden können, die folgende Qualitäten aufweist (siehe Wirbelndes Licht - Die komplexe Grundstruktur
unseres Lebens):
sie ist:
Die Sprache bzw. die Gedanken des Menschen kann man entsprechend einer Interpretation von Herbert Guenther als Prozess aus ontischer Sicht wie folgt charakterisieren:
Die hier in Grafiken verwendeten Iterationsverfahren basieren auf dem von Michael F. Barnsley beschriebenen Fluchtzeitalgorithmus. Die Berechnung von Endergebnissen nach Vorgabe einer Anzahl von Iterationen führen dabei bei einer konstanten Störgröße c zu unterschiedlichen Ergebnisklassen, wobei sich bei einigen Julia-Funktionen bei der Berechnung unter den Bedingungen der Hausdorff-Metrik Mengen mit kontraktierenden Berechnungsergebnissen herauskristallisieren, deren Grenzwerte zu Fixpunkten führen, die auch als Attraktoren bezeichnet werden:
Ralf Otte interpretiert die Bildung eines Attraktors (Typ 1) als das Erkennen als Folge einer Wahrnehmung bzw. eines Gedanken; Typ 2 als das
Alternieren von Wahrnehmungen/Gedanken; Typ 3 als einen permanenten Fluss diskreter Zustände. Ausgehend von unbewussten Zuständen entspricht die Iteration
einem rekursiven dynamischen Prozess, der bei der Konvergenz zu einem Attraktor als vorbewusster Zustand gedeutet wird. In Konkurrenz und Überlagerung mit
anderen vorbewussten Zuständen (z.B. Erinnerungen) kann nach einer Wechselwirkung über die von Ralf Otte beschriebene Aufmerksamkeitsfunktion der Iterationsprozess zu einem
bewussten mentalen Zustand kollabieren, bis schließlich neue Wahrnehmungen zu einem neuen Iterationsprozess führen.
Michael F. Barnsley hat gezeigt, dass die
Abbildung der Ergebnisse der Iterationen auf eine Riemannnsche Sphäre unter der Menge Ĉ (mit Ĉ := ℂ ∪ ∞) zu einem attraktiven Fixpunkt bei 0 (Südpol) führt und beim Fluchtverhalten bei ∞ zu
einem repulsiven Fluchtpunkt am Nordpol. Übertragen auf eine Ebene entspricht diese Dynamik einer einfachen Möbiustransformation, bei der sich die Bildung der
attraktiven Fixpunkte in Gestalt einer iterierenden Spirale vollzieht.
Heinz-Otto Peitgen hat außerdem gezeigt,
dass Iterierte Funktionensysteme nicht nur zu invarianten Punkten führen können, sondern statt dessen mehrere oder sogar unendlich viele Attraktoren
besitzen können. Weiter unten werden einige Beispiele gezeigt.
Zunächst einige Beispiele, bei denen Attraktoren gebildet werden. Dabei wird die Störgröße c derart gewählt, dass als Ergebnis Julia-Mengen und -Flächen gebildet werden. Die
Störgröße c wird in diesen Beispielen auch gleichzeitig als Startwert für die Berechnung des Attraktors verwendet. Grundsätzlich gilt, dass die gesamte innere Fläche
der Julia-Funktion einem Attraktor entspricht. Bei den hier verwendeten Einzelberechnungen von Attraktoren werden
die Iterationsschritte durch (transparente) Linien, Punkte, Symbole und Farben kenntlich gemacht.
Symbolik:
Zunächst werden Beispiele für verschiedene Attraktoren und Trajektorien gezeigt,
bei denen noch kein Bezug auf die Zahl der von Lama Anagarika Govinda
beschriebenen Schwingungen genommen wird.
Bild 1 zeigt die Bildung einer Trajektorie in einen Attraktor bei 50 Iterationen. Dabei zeigt sich eine um einen
Mittelpunkt bestehende Schwingung der einzelnen Iterationsschritte mit abnehmender Distanz vom Mittelpunkt.
Ein abschließender zentraler Mittelpunkt hat sich noch nicht gebildet (roter Endpunkt). Nach 500 Iterationen (Bild 2) erreicht der
Hutchinson-Operator W eine weitere Annäherung an den Mittelpunkt (fast zentraler roter Endpunkt).
Bild 3 zeigt die Vergrößerung des zentralen Bereichs der Trajektorie. Der Endpunkt strebt auf einen zentralen Punkt zu. Die Anordnung
der Zwischenergebnisse aus den einzelnen Iterationsschritten (graue Punkte) lässt vermuten, dass man die gesamte Julia-Menge bzw. Fläche in
eine Schwingung versetzen kann, indem man die Störgröße c nach jedem Iterationsschritt auf das letzte Zwischenergebnis setzt: ci+1=ci
In den Bildern 1-3 zeigt sich, dass einige wenige Zwischenergebnisse der Iteration (graue Punkte) nicht jeweils eine Eingangs- und Ausgangslinie aufweisen, sondern
anscheinend nur eine Verbindungslinie aufweisen. Hier wäre zu prüfen, ob Ein- und Ausgang auf einer Geraden liegen oder sogar zum Vorgängerpunkt zurück führen.
Bild 4 zeigt eine stark alternierende Trajektorie, die sich keinem zentralen Attraktorpunkt annähert. Auch hier wäre noch zu prüfen, welche Arten
von Schwingungen entstehen, wenn man die Störgröße nach jedem Iterationsschritt auf das Vorgängerergebnis setzt: ci+1=ci
Bild 5 zeigt ansatzweise einen Orbit dicht an der Julia-Menge, der allerdings bereits nach wenigen Iterationen als Fluchtpunkt endet und somit einem
Seltsamen Attraktor nur ansatzweise nahekommt. (Der rote Endpunkt liegt knapp
außerhalb der umhüllenden Menge der Julia-Menge, so dass der Berechnungsalgorithmus hier abbricht).
Bei den Bildern der Serie 2 wurden als Samples für die Berechnung von Trajektorien gitterförmig Startwerte angelegt, von denen aus die einzelnen
Trajektorien in das Bild projiziert werden. In Abhängigkeit von der Darstellungsvariante können Endpunkte der
Trajektorien (rot) ebenfalls angezeigt werden. Wegen der Dichte der Zwischenergebnisse werden keine grauen Markierungen mehr angezeigt und auch die exakten
Startpositionen werden nicht hervorgehoben; es
werden lediglich Trajektorien und ggf. die Endpunkte angezeigt.
Die Endpunkte (rot) müssen bei einigen Einstellungen außerdem
algorithmisch reduziert werden, damit nicht überladene Rasterflächen entstehen. Der Algorithmus reduziert aus optischen Gründen außerdem Endpunkte, die zu dicht ( < 3 Pixel )
am Startpunkt der Trajektorie liegen.
Bild 1 enthält dieselbe Störgröße wie bei Bild 1 aus Serie 1. Bei 50 Iterationen und 40401 Trajektorien zeigt sich auch hier, dass ein
Attraktor mit einem einzelnen Endzustand nicht existiert. Vielmehr wird ein Attraktorbassin im Innern der Julia-Fläche sichtbar und viele Fluchtpunkte
außerhalb der Julia-Menge.
Bild 2 enthält eine Ausschnittsvergrößerung aus dem Attraktorbassin von Bild 1. Die sich ergebenden Muster von Endpunkten variieren allerdings bei unterschiedlichen
Einstellungen im Hinblick auf die Zahl von Trajektorien und Vergrößerungen; hier gezeigt wird aber lediglich das gewählte Beispiel mit den genannten Einstellungen.
Bei Bild 3 wurde die Zahl der Trajektorien bei gleichem Maßstab und Ausschnitt wie bei Bild 2 auf 167 reduziert, wobei aber gleichzeitig nur Startwerte
auf der realen Achse zugelassen wurden. Hierdurch wurde die Struktur der Trajektorien der realen Achse hervorgehoben und die Struktur der Endpunkte reduziert.
Bild 4 zeigt Trajektorien, die weitgehend in Richtung ∞ streben.
Hier wurde eine Störgröße gewählt, bei der keine Julia-Menge mehr entsteht, und ein
Maßstab gewählt, der einen Blick auf ein äußeres Gebiet zulässt. Bei dieser Einstellung
gibt es hier keine Cauchy-Folgen mehr, die zu gefangenen Punkten innerhalb einer Julia-Menge führen.
In Bild 5 werden zusätzlich die Fluchtpunkte ausgegeben, die nicht sofort in Richtung unendlich weisen.
Es zeigt sich, dass sich scheinbare Häufungspunkte bzw. ein repulsives Attraktorbassin
auch außerhalb einer Julia-Fläche bilden können.
Eine mögliche Bedeutung eines derartigen Häufungspunktes und derartiger Trajektorien im Hinblick auf Unbewusstes wäre zu klären.
Bild 5 aus Serie 1 (oben) zeigt als Folge der gewählten Störgröße eine Struktur der Julia-Menge, die lediglich Fatou-Staub aufweist.
Daher werden hier noch ein paar Darstellungen dieser Struktur in
Verbindung mit Trajektorien vorgenommen.
Bei Bild 6 wurden nur 4 Iterationen durchgeführt, die noch Wahrscheinlichkeitsdichten aufweisen, aus denen sich nach dem Modell vom
Lama Anagarika Govinda Beobachtungen im virtuellen
Beobachtungsraum ableiten lassen sollten. Dargestellt ist ausschließlich eine Reihe von Trajektorien, die auf der realen Achse beginnen. Die Endpunkte
aller Tajektorien sind rot markiert. Die zentrale rote Linie stellt diejenigen dicht beieinander liegenden Endpunkte dar, die auf der Realachse gestartet
wurden und sofort wieder terminieren. Trajektorien innerhalb der ε-Sphäre führen teilweise zu Endpunkten, die noch innerhalb der ε-Sphäre liegen. Der
Versatz paralleler, senkrechter Linien mit undefinierten Werten lässt vermuten, dass die Ursache in der Beschränktheit der Gleitkommamenge G und ihren
Rechenregeln liegt. Die eigentliche Julia-Menge erscheint hier als rote Grenzlinie.
Bei Bild 7 wurden die Trajektorien auch für die imaginären Werte gebildet. Hierbei zeigt sich ein Attraktorbassin innerhalb der ε-Sphäre.
In Analogie zu den Phasen der Bewusstwerdung findet nach Lama Anagarika Govinda mit der 4. Schwingung die Gewahrwerdung beim Prozess
der Bewusstwerdung statt.
Im Vergleich dazu werden mit den Bildern 8 und 9 Trajektorien mit 50 Iterationen gegenübergestellt. In Bild 8 kann man die zunehmende Ausbildung
eines Seltsamen Attraktors als Abhängigkeit vom Startpunkt der Trajektorie erkennen, wobei sich aber die eigentliche Julia-Menge bis auf etwas Fatou-Staub schon
weitgehend aufgelöst hat. Bei Bild 9 sieht man, dass das Attraktorbassin den
zentralen Bereich der ε-Sphäre verlassen hat. Einige Endpunkte der Trajektorien liegen aber dennoch innerhalb der ε-Sphäre, so dass
man vermuten kann, dass hier Ergebnisse entstanden sind, die auf vorbewusste geistige Zustände gemäß der Interpretation von Ralf Otte hinweisen.
(Zur besseren Sichtbarkeit der Endpunkte der Trajektorien innerhalb der ε-Sphäre wurden die grauen Trajektorien teilweise stark gedimmt.)
Bei 4 Iterationen zeigen die Wahrscheinlichkeitsdichten in kleinen Gebieten Werte, die grundsätzlich eine Messung ermöglichen sollten. Diese Messbarkeit
nimmt aber mit steigender Iterationszahl ab, wie schon in Abschnitt 7 "Grenzwerte" gezeigt:

Der Verlauf der Trajektorien insgesamt lässt die Vermutung zu, dass ein Iterationsablauf bei veränderlicher Störgröße mit ci+1=ci sich ein
selbstregulierendes, bisweilen schwingendes Systemverhalten zeigt, bei dem sich die Struktur der Julia-Menge in vielen Fällen selbst stabilisiert,
solange die Ergebnisse der Iterationen einer Cauchy-Folge entsprechen und sich auflöst, wenn keine Cauchy-Folge vorliegt.
Im Raum steht auch noch das Postulat, dass die semantischen Inhalte von Gedanken und Gedankenfolgen, -ketten
sowie der Denkprozess an sich, die sich nach Ansicht im Dzogchen auf Basis einer
inhärenten sich selbst organisierenden Intelligenz bilden und ausdrücken, durch Wahrscheinlichkeiten selektiert werden und sich selbstorganisierenden Schwarmregeln
unterliegen können. Um hier einen Schritt weiter zu kommen, macht es Sinn, die Trajektorien, die in den Bildern
Strukturen aufweisen, auf mögliche Regeln zu untersuchen. Als Analogie zu diesen Trajektorien kann man das folgende Video über das herkömmliche Schwarmverhalten mit der
Gradientenregel (nach Craig Reynolds) ansehen, bei dem Nachbarschaftsgruppen ebenfalls zu virtuellen
Trajektorien führen, die den Trajektorien in den Bildern oben ähneln
(zur Reduzierung von Rechenzeiten besitzen die Boids für Richtungswechsel lediglich 8 Freiheitsgrade,
woraus teilweise eckige Bewegungen hervorgerufen werden) :
Entstehen und Vergehen von Nachbarschaftsgruppen
Anzahl Boids: 1500
Sichtfeld eines Boid: 90 Grad
Blickweite eines Boid: 200 Pixel
Laufgeschwindigkeit eines Boid: konstant
Richtungsentscheidung eines Boid: Gradientenregel
Größe einer Nachbarschaftsgruppe: 15 Boids
Farben/Symbolik:
blau: vollständige Nachbarschaftsgruppe
grau: unvollständige Nachbarschaftsgruppe
grün: Kollision
rot : Boid
blaue oder graue Quadrate: Schwerpunkt der Nachbarschaftsgruppe
blaue oder graue Linie: Zielrichtung (Gradient) der Gruppe
Nadelspitze: Zielposition der Nachbarschaftsgruppe
Dauer (0:31 min)
Bei Betätigung des Start-Buttons erfolgt der Zugang zum YouTube-Video, wobei die IP durch YouTube registriert wird und weitere Auswertungen
durch YouTube erfolgen (siehe Impressum)
In dem obigen Video sind allerdings nicht die Trajektorien selbst dargestellt, sondern stattdessen in grafischer Form die durch Schwarmregeln hervorgerufenen Entscheidungsprozesse
der Boids vor dem Zeitpunkt der endgültigen Richtungsentscheidung. Hierdurch zeigen sich als Übersicht
die Bewegungen der Boids und das Schwarmverhalten als Ganzes.
In einem zweiten Video sind die Pfade der Boids dargestellt, die in Analogie den Trajektorien bei den Julia-Mengen oben entsprechen. In diesem 2. Video wird aus Gründen der
besseren Sichtbarkeit lediglich für ein einzelnes Boid-Individuum das Erkennen der Nachbarschaftsbeziehungen und dem sich daraus ergebenden Gradienten hervorgehoben:
Trajektorien (Pfade) in Schwärmen
Anzahl Boids: 250
Sichtfeld eines Boid: 360 Grad
Blickweite eines Boid: 200 Pixel
Laufgeschwindigkeit eines Boid: variabel
Richtungsentscheidung eines Boid: Gradientenregel
Größe einer Nachbarschaftsgruppe: 7 Boids
Farben/Symbolik:
rote Punkte : Boids
Gelbtöne: Vergangenheitspfade der Boids; hellgelb: aktuell; Grautöne: Zeitverlauf für ältere Vergangenheitspositionen
Einzelnes Boid-Individuum:
türkisfarbene Vergangenheitslinie: hervorgehobener Einzelpfad des Boid-Individuums
türkisfarbene Zukunftslinie: hervorgehobener Ziel-Gradient des Boid-Individuums
dunkelblaue Linie: abschließend gewählte Richtung nach Richtungsentscheidung des Boid-Induividuums
grünes Quadrat: Schwerpunkt der Nachbarschaftsgruppe des Boid-Individuums
grüne Linie: Zielrichtung (Gradient) der Nachbarschaftsgruppe des Boid-Individuums
grüne Nadelspitze: Zielposition der Nachbarschaftsgruppe des Boid-Individuums
kurze graue vom Boid-Individuum ausgehende Linien: erkannte und ausgewählte Nachbarn, die die Nachbarschaftsgruppe bilden
kurze graue von den Boids der Nachbarschaftsgruppe ausgehende Linien: Zielrichtungen (Gradienten) der erkannten und ausgewählten Nachbarn
kleines rotes Quadrat: Zentralposition des Beobachtungsfeldes
größeres rotes Quadrat: Schwerpunkt des Gesamtschwarms
Dauer (0:14 min)
Bei Betätigung des Start-Buttons erfolgt der Zugang zum YouTube-Video, wobei die IP durch YouTube registriert wird und weitere Auswertungen
durch YouTube erfolgen (siehe Impressum)
Die Videos mit dem Schwarmverhalten und der Hervorhebung von Trajektorien ähneln in ihren Algorithmen dem Aufbau des Bewusstseinsmodells von Ralf Otte mit seinem
Möglichkeitsfeld, der Übertragungsfunktion und dem virtuellen Beobachtungsfeld. Die kleinen roten Punkte im Video zeigen die scheinbar real vorhandenen Boids, die
in unserer als real erscheinenden Umwelt einzelnen Schwarmmitgliedern (z.B. Fische) entsprechen. Der Prozess des Erkennens von Nachbarn, ihrer Bewegungsrichtung, der Abschätzung
von Kollisionen, der Bewegungsannäherung auf einen Zielpunkt entspricht in Analogie der Übertragungsfunktion von Ralf Otte, bei der es zu einem Bewusstwerdungsprozess
kommt. Die letztendliche Entscheidung über eine einzuschlagende Zielrichtung erfolgt aber unter der Kontrolle derjenigen Schwarmregeln, die man als
inhärent im Möglichkeitsfeld ansehen kann,
wobei aus den potenziellen Bewegungsmöglichkeiten diejenige ausgewählt wird, die am besten zu den inhärenten Schwarmregeln passt. Somit entspräche dieser
letztendliche Entscheidungsprozess
einem Vorgang innerhalb des Möglichkeitsfeldes, der Vorrang zu einer beabsichtigen Bewegung besitzt. Diese letztendliche Entscheidung entspräche damit auch
einer Entscheidung bzw. eines Impulses auf Basis eines 1. Nen nach Katsuki Sekida, während die Ergebnisse aus den sonstigen Schwarmregeln einem 2. Nen entsprechen.
Auch beim Menschen kann man einen vergleichbaren Entscheidungsprozess über die Libet-Experimente nachweisen (mit all den
daraus sich ergebenden philosophischen Konsequenzen).
Ein wesentlicher Unterschied zu dem Modell von Ralf Otte besteht darin, dass die Berechnungen hier nicht mehr auf der Menge ℂ der komplexen Zahlen und
ihrer hyperkomplexen Algebra beruhen, die bei der Umsetzung mit Software zu
Einschränkungen durch Anwendung von Gleitkommaregeln und der Menge der Gleitkommazahlen G führen, sondern hier in dem Schwarmmodell auf der Menge der ganzen Zahlen ℤ
in Verbindung mit einer erweiterten Manhattanmetrik beruhen, die auch diagonale Bewegungen in einem Step zulässt. Als Konsequenz ergibt sich bei dem Schwarmmodell die Simulation
in einer 2-dimensionalen Ebene (, die man mit erhöhtem Softwareaufwand in eine 3-dimensionale Simulation überführen könnte,) gegenüber dem Modell mit komplexen Zahlen, das
sich in der 1. Dimension auf den Realanteil bezieht und in der 2. Dimension auf Wahrscheinlichkeiten bezieht. Weil man aber davon ausgehen kann, das auch bei
Erhöhung von Dimensionen die Grundstruktur von Erscheinungsbildern grundsätzlich Gemeinsamkeiten aufweist, lassen sich auch Vergleiche zwischen diesen Modellen
ziehen.
Das Schwarmmodell zeigt den Wechsel zwischen dem Möglichkeitsfeld und einer bidirektionalen Übertragungsfunktion, bei der die alten und neuen Positionen der Boids
zwischen dem virtuellen Beobachtungsfeld und dem Möglichkeitsfeld hin und her gespiegelt werden. Die Wahrscheinlichkeiten aus dem Möglichkeitsfeld und ihre
Selektion als Entscheidung ergeben sich dabei aber aus den Schwarmregeln, die in der Schwarmsimulation algorithmisch vollzogen
werden.
Für den gesamten Prozess des Schwarmverhaltens besteht aus Sicht eines jeden Boids auch eine Beziehung zu den im Abschnitt 5 ("Simulationen")
beschriebenen Skandha:
Lediglich bei Lebewesen mit einer
Reflexionsfähigkeit des eigenen Bewusstseins und der reflexiven Erkenntnis aus einer Selbstbeobachtung (3. Nen im Modell von Katsuki Sekida) kann unter
Umständen die Entscheidung im Unbewussten kurz vor der sich daraus ergebenden Handlungsausführung unterbrochen werden, so dass ein neuer
Entscheidungsprozess oder eine alternative intuitive Entscheidung zur Ausführung gebracht werden kann. Es ist davon auszugehen, dass diese Entscheidung
zeitlich bereits vor Eintreten des 4. Skandha im Unbewussten geschieht. Das Wirken der Skandha 1-4 entspräche damit den Vorgängen in der Übertragungsfunktion und
im virtuellen Beobachtungsfeld und denjenigen Schwarmregeln, die mit Wahrnehmung und Erkenntnis (also dem Intellekt im Sinne eines reflexiven Erkennens) zu tun haben;
die inhärente Entscheidungsfindung auf Basis
grundlegender Schwarmregeln im Dharmakaya entspräche dann einem Impuls der nicht-energetischen Wellenfunktionen im Möglichkeitsfeld.
Laut Chögyam Trungpa besteht ein reger Wechsel zwischen den 3 Kayas in beide Richtungen.
Übertragen auf das Modell von Ralf Otte sollte daher auch dort ein bidirektionaler Wechsel mittels der Übertragungsfunktion erfolgen. Im Dzogchen geht man
letztendlich (nach James Low oder Tenzin Wangyal Rinpoche)
davon aus, dass das Modell der 3 Kayas seinen wesentlichen Sinn darin erfährt, Meditierenden die Qualitäten der 3 Kayas erfahren zu lassen, um daran anschließend
zu erkennen, dass die 3 Kayas ein Konzept innerhalb eines einzigen "Raumes" darstellen, dem Dharmadhatu, aus dem alle Erscheinungen hervorgehen.
Um in einer ersten Annäherung zu sehen, ob es Ähnlichkeiten oder sogar Homologien zwischen Schwarmintelligenz und den anderen Modellen gibt, werden in den folgenden Beispielen
die sich ergebenden Unterschiede innerhalb von Schwärmen gezeigt, die durch Variation der Schwarmregeln zu unterschiedlichen
Schwarmstrukturen führen und auch den Einfluss der Trajektorien durch die Gradientenregel erkennen lassen. Die Schwarmregeln selbst (z.B. Kohäsion, Separation oder
Alignment nach Craig Reynolds) sind hier allerdings nicht weiter beschrieben.
Symbolik:
Bild 1 zeigt die Trajektorien auf Basis der Gradientenregel bei einem Sichtfeld der Boids von 90 Grad, wie man es bei vielen Tierschwärmen vorfinden kann. Das Bild
zeigt eine Aufteilung eines Schwarms in 2 Teilschwärme.
Bei Bild 2 wird gegenüber Bild 1 der Einfluss des Sichtfeldes auf die Schwarmstruktur bzw. das Schwarmverhalten gezeigt (wie beispielsweise bei
einigen Fischarten). Hier ist der Schwarmzusammenhalt größer als bei einem kleineren Sichtfeld.
Bei Bild 3 wird an Stelle der Gradientenregel die Schwerpunktregel bei einem Sichtfeld von 90 Grad gezeigt, die zu vollkommen anderen Schwarmstrukturen führt,
die man eher bei Insekten vorfinden kann.
Bei Bild 4 wird ebenfalls die einfachere Schwerpunktregel verwendet aber bei Nachbarschaftsbeziehungen mit nur 6 Nachbarn, wie man sie häufiger in Tierschwärmen vorfindet.
Hier in Bild 5 hat der Winkel des Sichtfeldes erheblich größere Auswirkungen auf die Schwarmstruktur. Es bilden sich viele kleine Teilschwärme,
da nun die Schwerpunkte eng beieinander
liegen und keine Trajektorien gebildet werden ähnlich wie bei Feuerfliegen (Photinus Carolinus). (Die Feuerfliegen sind allerdings in der Lage, sich zusätzlich über periodische
Leuchtsignale mittels Biolumineszenz zu synchronisieren, was ihnen erlaubt bei Dunkelheit Schwarmregeln zu befolgen.)
Die Anzahl vorhandener Boids sowie die Anzahl der Nachbarn, aus denen sich eine Nachbarschaftsgruppe zusammensetzt, bestimmen ebenfalls die Struktur von Schwärmen (Bild 6 und 7).
DIe Gegenüberstellung bei kleinerer Schwarmgröße mit Gradientenregel und unterschiedlichem Sichtfeld zeigen die Bilder 8 und 9. Hier sind die Unterschiede ebenfalls
erkennbar wie bei den Beispielen von Bild 1 und 2. Das größere Sichtfeld der Boids (Bild 9) führt hier ebenfalls zu einer höheren Dynamik im Schwarm ähnlich wie bei Bild 2.
Bei Bild 9 bildet sich aus 2 Teilschwärmen ein gemeinsamer Schwarm. Bild 8 zeigt eine (vorübergehende) Konzentration auf einen (vorübergehenden) gemeinsamen
Schwarmschwerpunkt, der von den Boids aber bei den hier verwendeten Schwarmregeln selbst nicht erkannt werden kann. Als Folge einer hier verwendeten Mindestabstandsregel wird sich
der gemeinsame Schwerpunkt in Kürze wieder auflösen.
Weitere Dynamisierungen, die in diesen Grafiken aber nicht dargestellt sind, werden sichtbar, wenn man zusätzlich variable Geschwindigkeitsregeln
für die Boids zulässt; die Grundprinzipien der
Schwarmbildung bleiben dabei aber weitgehend unverändert.
Im Vergleich zu den grafischen Darstellungen mit den Trajektorien bei Julia-Funktionen ergeben sich größere (optische) Übereinstimmungen bei Schwarmregeln,
die die Gradientenregel verwenden.
Zu untersuchen wäre, welche Analogien zwischen der Auswahl einer Entscheidung vor Beginn der Iteration - also vor dem ersten sich ereignenden Startwert der Julia-Funktion auf
Basis von Wahrscheinlichkeitswerten - und der
Anwendung einer Schwarmregel inkl. inhärenter vorrangiger Entscheidung bestehen. Im Schwingungsmodell von Lama Anagarika Govinda entspräche das möglichen Vorgängen vor
Beginn der ersten Schwingung. Im Modell von Katsuki Sekida würde die spontane Entscheidung oder ein Impuls im Unbewussten ohne weitere Untergliederung unter dem 1. Nen subsumiert.
Der größte Unterschied zwischen den Darstellungen von Wahrscheinlichkeitsdichten mit ihren Attraktoren und Trajektorien im Möglichkeitsfeld und den Schwarmbildern besteht in der
Verwendung der zugrunde liegenden Zahlenmengen: dort ℂ, hier ℤ X ℤ und den fehlenden Wahrscheinlichkeitswerten im Schwarmmodell. Die Situation ist vergleichbar
mit der im Abschnitt 6 ("Spiegelung") beschriebenen realen Achse im Beobachtungsfeld
nach Anwendung eines künstlichen neuronalen Netzes auf die im Wahrscheinlichkeitsfeld
vorliegenden Werte. Somit kann man die Schwarmbilder als Bestandteil einer Spiegelung sehen, wobei aber die Übertragungsfunktion bisher unbekannt ist. Allerdings
verwendet die Simulation von Schwärmen ebenfalls Wahrscheinlichkeiten auf ihrer Ebene des Dharmakaya und auch auf der Ebene der Skandha, die dem virtuellen Beobachtungsfeld
entsprächen.
Die hier aufgeführten Analogien stellen allerdings lediglich einen Hinweis dar, dass Iterierte Funktionssysteme mit Regeln der Schwarmintelligenz
übereinstimmen könnten, wobei bislang unklar bleibt, wie Schwarmregeln aussehen müssten, um Julia-Fraktalen zu entsprechen, und umgekehrt, wie Julia-Funktionen oder
andere Iterierte Funktionensysteme Schwarmstrukturen abbilden könnten.
Bei beiden Vorgehensweisen handelt es sich aber um reduktionistische Modelle, die nicht der Wirklichkeit entsprechen, sondern nur versuchen,
einen Hinweis auf Prozesse in der Natur zu geben; etwa in dem Sinne, wie ein Wegweiser, der nicht das Ziel darstellt, sondern nur einen Hinweis gibt, wo das Ziel
möglicherweise gefunden werden
kann. Nach Ansicht des Dzogchen ist eine Beschreibung niemals in der Lage, auch das Ziel zu sein, sondern jede Beschreibung, jedes Gedankenkonstrukt,
jedes Konzept stellt immer nur einen Wegweiser dar.
Einen Hinweis, wie Nachbarschaftsbeziehungen bzw. Schwarmregeln auf Ebene von Möglichkeitsfeldern aussehen könnten, kann man eventuell auch aus Interpretationen
von David Bohm mit der von ihm beschriebenen impliziten Ordnung
ableiten; das wurde hier nicht aber weiter untersucht.
Eine Selektion des jeweils nächsten Gedankens allein auf Basis einer ausschließlich stochastischen Zufallsentscheidung ist als Folge des
Infinite-Monkey-Theorems nicht möglich. Denkbar wäre allenfalls
beim Kollaps der Iterationsfolge eine passende Verformung desjenigen Wahrscheinlichkeitsfeldes im Möglichkeitsfeld (d.h. die Julia-Fläche),
die zu einer neuen Folge z0 beginnend mit Wahrscheinlichkeitswerten, bei denen die Selektion
des Folgegedankens eine Referenz zur vorherigen Folge besitzt. Aber für ein derartiges Verhalten der Gedankenfolgen auf Basis von Wahrscheinlichkeiten allein müssten
erst plausible Folgen von Iterationsfolgen mit geeigneten Kollapsbedingungen gefunden werden.
Die Selektion auf Basis von Schwarmregeln in Kombination mit Wahrscheinlichkeiten erscheint aussichtsreicher,
eine Lösung für das Infinite-Monkey-Theorem zu finden und gleichzeitig ein sich selbst organisierendes System hervorzurufen.
Abschnitt 9 "Bewusstwerdung" zeigt Beispiele, wie ein derartiger Prozess aussehen könnte.
Als Analogie ist aber auch noch das Verhalten makroskopischer Körper zu erwähnen, deren Bewegungsverhalten durch Schwerkraftgesetze beeinflusst wird. Bei bereits nur 3
Körpern ist eine Voraussage über den Entwicklungsprozess der Bewegungen nicht mehr möglich. Kleinste Änderungen der Anfangsbedingungen führen zu einem
chaotischen Bewegungsverhalten. Franziska Konitzer beschreibt die Problematik dieses Verhaltens und Versuche mit
statistical-escape-Therorien, wobei
sich Lösungsansätze mit Methoden der statistischen Mechanik ergeben, die auf Regelmäßigkeiten bei chaotischem Verhalten hinweisen.
Sie berichtet von den Ergebnissen eines Teams um Alessandro Alberto Trani, das bei den Berechnungen Wahrscheinlichkeitsverteilungen gefunden hat, die Zonen einer
Insel der Ordnung in einem Meer des Chaos ergeben, wobei allerdings eine Einzelvorhersage weiterhin nicht möglich ist. Die Zonen mit den Inseln der Ordnung weisen auf
eine gewisse Ähnlichkeit mit den Zonen konvergierender Ergebnisse innerhalb von Julia-Flächen auf. Während bei den Drei-Körperproblemen Schwerkräfte das Verhalten
beeinflussen, handelt es sich aber bei dem Möglichkeitsfeld Ralf Ottes mit Julia-Mengen um das Verhalten nicht-energetischer Wellen. Ralf Otte weist in seinem Ansatz
über die Simulation des Geistes allerdings auf statistische Einflüsse aus dem virtuellen Beobachtungsfeld hin, die die Form von Julia-Flächen mit ihren
messbaren Wahrscheinlichkeiten beeinflussen können. Ob die Ähnlichkeit derartiger Einflüsse bei materiellen und geistigen Feldern (z.B. im Vakuum) gleichartigen
Gesetzen unterliegt, bleibt allerdings offen.
Eine Angleichung zwischen dem Modell von Ralf Otte mit den Modellen der Drei Nen oder dem Schwingungsmodell von Lama Anagarika Govinda im Hinblick auf Gedankenprozesse
ist möglicherweise noch schwieriger.
Der Fluss der Gedanken, der sich durch die Drei Nen abbilden lässt, wird im Modell von Ralf Otte nicht direkt sichtbar, zumal hier intensiv der Wechsel zwischen
Möglichkeitsfeld und Beobachtungsfeld über die Übertragungsfunktion das Erkennen des Flusses erschwert. Katsuki Sekida hat aber auch eine spezielle Folge
von Nen beschrieben, bei der lediglich eine Kette der 1. Nen auftritt. Hierbei handelt es sich ausschließlich um nicht-konzeptuelle Gedanken, die unbewusst
und spontan ablaufen.
Das gezielte Ausschalten des 2. und 3. Nen ist dabei nur erfahrenen Meditierenden möglich. Die unbewusst/spontan entstehenden Gedanken sind unabhängig vom konzeptuellen Ich.
Nach Chögyam Trungpa sind sie Bestandteil einer eigenen selbst-existierenden Intelligenz, aus der auf Basis einer Art bidirektionaler Verbindung (Übertragungsfunktion)
zwischen Zufall im Sinne einer Wahrscheinlichkeit (Möglichkeitsfeld) und einem freien Willen Gedanken im virtuellen Beobachtungsfeld spontan entstehen. Er sieht den Grund
für diese Art des Denkens in einer bestimmten, selbst-existierenden Intelligenz, die mit der Gesamtheit in Verbindung steht, die präziser ist, die nicht verbal ist.
Diese Form unbewusster/spontaner Gedanken und Impulse sowie den damit verbundenen Entscheidungen entspricht dabei dem Entscheidungsvorgang bei den Libet-Experimenten, die zeitlich vor einer
konzeptuellen Entscheidung eines scheinbaren, konzeptuellen Ich entstehen.
Einen Hintergrund für diese Form nicht-bewusster Vorgänge, nicht-bewussten Handelns, nicht-bewusster Gedanken und Entscheidungen liefern die Messungen des
Systemneurowissenschaftlers György Buzsáki. Aus seinen Messungen neuronaler Aktivitäten ging hervor,
dass das früher bestehende Outside-In-Modell über die Wahrnehmung sensorischer Eindrücke in Verbindung mit Entscheidungen auf Basis eines freien Willens durch einen
angenommenen Beobachter im Geist zu Widersprüchen beim Erkennen von Objekten führt.
Sein Resumee lautet: Neuronen in den visuellen Arealen im Kortex und auch in dem hypothetisch angenommenen "Beobachter", der eingehenden Signalen eine Bedeutung zuweisen sollte,
können nicht "sehen", was in der Welt um sie herum geschieht. Es gibt keinen inneren Beobachter/Dolmetscher, der den sich ändernden Signalen der Neuronen eine Bedeutung
zuweisen kann.
Anstelle des widersprüchlichen Outside-In-Modells mit einem Beobachter beschrieb er ein Inside-Out-Modell, das ohne einen Beobachter auskommt und für das Erkennen/Sehen von Objekten
vom Neokortex veranlasste motorische Bewegungen (z.B. Augen, Muskeln) voraussetzt, die in Form von Efferenzkopien
zu einer (lernenden) neuronalen Verarbeitung führen, bei
der Informationen mit sensorischen und übergeordneten Hirnbereichen geteilt werden.
Der hier beschriebene Sachverhalt zum freien Willen und dem Wahrnehmungsprozess stimmt mit Meditationsexperimenten überein. Wenn man beispielsweise bei einer bewegungslosen Meditation
die bewusst werdenden Gedankenflüsse stoppt, Identifikationen von Objekten stoppt, Wertungen und Beurteilungen unterlässt und schließlich auch das Beobachten unterlässt,
dann entsteht ein Zustand, bei dem nichts Dinghaftes mehr wahrgenommen wird. Es ist ein "Sehen, ohne etwas zu sehen", obwohl der Sehprozess weiterläuft; selbst Formen und Farben
werden nicht mehr bewusst wahrgenommen; stattdessen entsteht im Geist ein optisches Gesamtbild, bei dem keine Einzelheiten/Formen/Farben bewusst werden. Der bewegungslose
Zustand stellt sich beispielsweise ein, wenn die Augen nicht mehr auf einen Punkt gerichtet sind und nicht mehr fixiert wird. Wichtig ist dabei,
dass die Sakkaden im Auge zur Ruhe kommen.
Erst wenn es wieder zu Sakkaden kommt oder wenn ein bewegtes Objekt den Bildbereich der Augen durchquert (z.B. ein fliegender Vogel), entsteht eine neue Prozessfolge,
bei der Wahrnehmungen wieder andersartig verarbeitet werden, wobei diese Verarbeitung unbewusst oder auch bewusst erfahren werden kann. Diese Form der Wahrnehmung entspricht
dem 1. Nen von Katsuki Sekida, die in Abhängigkeit der Energie der Wahrnehmung als 2. und 3. Nen weiter bewusst werden kann. Auch das von György Buzsáki beschriebene Wirken
des unbewusst arbeitenden neuronalen Netzes kann durch diese Form der Meditation erfahren werden: bewegte Objekte, wie Blätter im Wind, führen dagegen nicht zur Unterbrechung
des "Sehens, ohne etwas zu sehen". Hier muss man davon ausgehen, dass das unbewusst arbeitende neuronale Netz die Bewegung von Blättern zwar erkennt, aber auf der unbewussten Ebene als
nicht bedeutend bewertet. Diese Erkenntnis zeigt sich einem erst bei einer sofortigen Nachbetrachtung der Meditation beispielsweise nach erfolgter Wiederaktivierung der Sakkaden.
Untersuchungen eines Teams um den Neurobiologen David J. Freedman ergeben Hinweise, dass Entscheidungs- und Denkvorgänge auf bestimmten Strukturen
(Colliculli superiores) im
evolutionär alten Stammhirn beruhen, die von den Denkvorgängen der Großhirnrinde unabhängig verlaufen und nicht bewusst werden. Hieraus ergibt sich ein weiteres Indiz für
die Vorgänge bei den Libet-Experimenten. Diese Ergebnisse könnte man sowohl dahingehend deuten, dass die von Chögyam Trungpa genannte eigene selbst-existierende Intelligenz,
die separat von konzeptuellen Gedankenprozessen besteht, Bestandteil des Stammhirns ist, als auch dass das Stammhirn lediglich eine Kommunikationsschnittstelle
für die eigene selbst-existierende Intelligenz darstellt.
Eine alternative Erklärung wird von Patrick Krauss und Achim Schilling vermutet, die auf Basis von Untersuchungen lokaler Feldpotenziale im Gehirn mittels künstlicher Intelligenz
Muster gefunden haben, die zeigen, dass das Gehirn dauernd Erfahrungen und Sinneseindrücke für die Berechnung möglicher Szenarien als "predicitive coding"
nutzt, so dass spontane Aktivitäten und Entscheidungen ohne Bewusstwerdung vorgenommen werden können.
Im Anhang I "Spontaneität versus Impulsivität"
wird dargestellt, wie derartige Prozesse sich mittels der Drei Nen abbilden lassen.
Der zumeist sehr schnelle Wechsel der geistigen Verarbeitung von nicht-bewusst zu bewusst, kann nicht direkt beobachtet werden
und ist auch indirekten Eigenbeobachtungen nicht zugänglich. Der Dzogchen-Lehrer
James Low benennt diesen Zustand als das Auftreten einer (kurzen) Ohnmacht hin zu einem bewussten Zustand. Buddhaghosa beschrieb diesen Wechsel im 5. Jahrhundert wie folgt (Übersetzung
durch Alois Payer):
Wenn, während so der kontinuierliche Ablauf der Unterbewusstseinsmomente geschieht, die Sinnesorgane der Wesen geeignet sind, ein Objekt aufzunehmen, dann findet, wenn ein Sehobjekt in den Gesichtskreis eintritt, bedingt vom Sehobjekt eine Anregung (ghattana) des physischen Sehorgans statt. Kraft dieser Anregung geschieht eine Erregung (calana) des Unterbewusstseins. Daraufhin bricht der Strom der Unterbewusstseinsmomente ab und es entsteht ein funktionales Geistelement (kiriya-mano-dhatu). Dieses macht dieses Sehobjekt zum Objekt und erfüllt die Funktion des Aufmerkens (avajjana), indem es gleichsam den Unterbewusstseinsstrom unterbricht.
Herbert Guenther beschreibt zu dieser Thematik im Anklang an die Sicht der Quantenphysik 3 Phasenräume mit dazwischen bestehenden Symmetriebrechungen
(Quelle: Wirbelndes Licht - Ton, Farbe und Selbstorganisation). Übertragen auf die Drei Nen
umfasst der Phasenraum zum 1. Nen das Unbewusste, das dem Dharmadhatu/dem Urgund, also dem Sein (gzhi), dem Dasein (gnas-lugs) und dem "Modus des Aufleuchtens"
(snang-lugs) entspräche. Jeder Phasenraum enthält das Potenzial aller Möglichkeiten.
Hieraus ergibt sich für den 2. und 3. Nen abhängiges Entstehen, also eine Ursache-Wirkungsbeziehung. Dagegen können für den 1. Nen im
Dharmadhatu keine Referenzpunkte oder konkrete Regeln und auch keine
Ursache-Wirkungsbeziehungen erkannt werden. Auch der Übergang/der Symmetriebruch zwischen dem 1. und dem 2. Nen sowie auch das Zustandekommen von Entscheidungen
in Verbindung mit dem Dharmadhatu sowie der potenziellen Bewusstwerdung des unbewussten 1. Nen entziehen sich der bewussten Wahrnehmung, bis sie schließlich als
2. oder 3. Nen als bewusst erkannt werden können.
Hieraus ergeben sich außerdem die oben erwähnten Aussagen Chögyam Trungpas, wonach Denkprozesse und Entscheidungen Ergebnis einer nicht bewussten selbst-existierenden
Intelligenz sind, an die sich im Bewusstsein konzeptuelle/intellektuelle Gedanken (im 2. und 3. Nen) anschließen!
Herbert Guenther beschreibt die Zusammenhänge und die Dynamik zwischen den 3 Kayas bzw. 3 Phasen als eigene Intelligenz, aus denen sich nur in Teilen eine eigene
Entscheidungsfreiheit ergibt (Quelle: Wirbelndes Licht - Ton, Farbe und Selbstorganisation):
... Auf die Tatsache der Untrennbarkeit und Unteilbarkeit dieser Stufen oder Phasen weisen die prozessorientierten buddhistischen Texte immer wieder hin. Eben diese Dynamik der Einwirkungen und Durchdringungen machen die Annahme eines außerstehenden Urhebers gänzlich überflüssig. Die zugrunde liegende Dynamik, die es ermöglicht, dass die Prinzipien der komplementären Ergänzung unsere erlebte Wirklichkeit organisieren, wird mit dem technischen Ausdruck rtsal "schöpferische Kraft" bezeichnet, welche autokatalytisch oder selbstregulierend als Intelligenz des Ganzen wirkt, als eine überbewusste ekstatische Intensität (rig-pa), deren Funktionen die verschiedenen Funktionen des Urwissens sind. Diese überbewusste ekstatische Intensität ist die eigene (rang) Intensität des Ganzen oder "Eigenintensität" (rang-rig). Obwohl diese Intensität das "Subjekt an sich" oder das Selbst ist, mit dem wir im allgemeinen unser Bewusstsein assoziieren, darf uns diese Gewohnheitstendenz nicht zur unfundierten und verfehlten Schlussfolgerung verleiten, das Bewusstsein sei gelenkt von Absichten oder von Zweckdienlichkeiten, denn diese letzteren Aspekte gehören einem weniger entwickelten Niveau der Psyche an.
In einem weiteren Essay (Wirbelndes Licht - Mandala und/oder dkyil-'khor) weist Herbert Guenther darauf hin, dass es sich bei der hier beschriebenen eigenständigen Intelligenz
um die Intelligenz des Universums/des Ganzen und damit auch der menschlichen, nicht egologischen Intelligenz handelt, die auch als Lebendigkeit und Prozess in Form einer kondensierten Energie
innerhalb des kosmischen Aspekts des anthropokosmischen Ganzen handelt. Daraus ergibt sich erneut die Frage, ob diese Form der Intelligenz einer Schwarmintelligenz entspricht und welche
(Schwarm-)Regeln in dieser Intelligenz wirken. Darüber hinaus stellt sich die weitere Frage, inwieweit die Form dieser Intelligenz Fraktalen entspricht. Wenn man die fraktalen Strukturen unserer Umwelt
betrachtet (z.B. Lungenbläschen, Blätter, Wurzeln oder auch Planeten oder Küstenlinien), die Phänomene des gespiegelten virtuellen Beobachtungsfeldes von Ralf Otte darstellen, dann
sollten derartige Fraktale auch im
nicht beobachtbaren Möglichkeitsfeld als intelligente "Strukturen" vorhanden sein, da aus dem Möglichkeitsfeld eine Spiegelung als Phänomene im virtuellen Beobachtungsfeld erfolgt.
Das Beispielbild zeigt, wie eine fraktale Struktur im Möglichkeitsfeld gebildet werden kann, die ihrerseits Ähnlichkeiten mit der Anordnung von Planeten und Schwerkraftfeldern aufweist.
Fraktale Strukturen als Intelligenz
mit der von Herbert Guenther beschriebenen schöpferischen Dynamik einer Autopoiesis und Lebendigkeit (rtsal), die Energiemustern entspricht, besitzen nach Herbert Guenther eine
dynamische (bewegte und bewegende) Stille in einem Zentrum, das ringsum von rastlosen Spannungen umgeben ist, wobei die im Zentrum (dkyil) weilende "Intelligenz" sich mit anderen
"Intelligenzen" umgibt ('khor), die in ihrer eigenen Dynamik untrennbar mit der im Zentrum weilenden Intelligenz verbunden sind. Diese Beschreibung lässt sich auch mit der
Anordnung von fraktalen Strukturen, wie sie von Ralf Otte mit Julia-Funktionen zur Modellierung des Bewusstwerdungsvorgangs verwendet werden, vereinbaren.
Viele der hier verwendeten Grafiken mit Julia-Funktionen weisen das Grundprinzip dieser Strukturen auf, obwohl diese lediglich 1-dimensionale Strukturen mit ihren Möglichkeitswerten wiedergeben;
die von Herbert Guenther beschriebenen Strukturen müssten allerdings in einem höherdimensionalen Raum wirksam werden.
Aus den von Herbert Guenther übersetzten Texten Padmasambhavas der spyi-ti und yang-ti Lehre geht hervor, das zwei widerspiegelnde Energiemuster
(das Energiemuster des Eigenzustandes und das widerspiegelnde Energiemuster) bestehen. Diese Energiemuster zeigen sich ebenfalls
in der Quantenphysik als beobachtetes System, dessen Eigenschaften nicht unabhängig von den Einwirkungen des beobachtenden Systems bleiben. Dieses widerspiegelnde Muster findet
sich ebenfalls in der hyperkomplexen Algebra von Ralf Otte wieder. Weitergehende Auslegungen, die versuchen die im Zentrum weilende Intelligenz und deren Dynamik zu beschreiben, findet man in
Texten Padmasambhavas bei Herbert Guenther (Wirbelndes Licht: Das Einzigartige als Unendlichkeit und Intensität).
Die selbst-existierende Intelligenz stellt sicherlich ein Problem in Hinsicht auf ihre Deutung für Philosophien und Religionen dar, das innerhalb der Glaubenssysteme
intellektuell gelöst werden muss, um nicht unglaubwürdig zu werden. Die theistischen Religionen haben es sich hier sehr leicht gemacht, indem sie als Absolutum
einen Gott kreierten, der seinerseits als Kreationist angesehen wird. Wie die Vergangenheit zeigt, wird jede alternative Ansicht hierzu als Häresie verdammt.
Beispielsweise hat Arno Borst den Protokollen der katholischen Inquisition entnommen, dass die Anhänger
von Almarich von Bene, die an der Pariser Universität
im 12./13. Jahrhundert als Amalrikaner wirkten, eine neue pantheistische Philosophie auf den Grundlagen von Aristoteles, Johannes Eriugena, der Schule von Chartres und Ben Gabirol
errichtet haben, bis die Amalrikaner durch die Inquisition auf dem Scheiterhaufen eliminiert wurden. Die neue Form des
Pantheismus hatte Bezüge zu den Zielen der
Waldenser und galt als Alternative zum damals ebenfalls bestehenden
Katharismus.
Der Pantheismus mit der Gleichsetzung von Gott, Natur und Mensch stand den machtbewussten Päpsten natürlich im Wege, da im Pantheismus ein Papst als Mittler zwischen Gott
und Mensch nicht mehr benötigt wird. Den meisten theistischen Religionen ist es bis heute nicht gelungen, die Erkenntnisse der Vergangenheit und auch die Aspekte
von Gott vs. Teufel bzw. eine übergeordnete Sicht von gut und schlecht in ihren Doktrinen aufzunehmen. Meister Eckhart,
der einige Zeit nach den Amalrikanern ebenfalls an der Pariser Universität Vorlesungen gehalten hat,
werden die Probleme mit dem Pantheismus und der Inquisition nicht verborgen geblieben sein. In seinen Ausführungen bleibt Meister Eckhart daher sehr vorsichtig. In seinem
Sermon XXIX "DEUS UNUS EST" beschreibt er das Wesen Gottes, das bei herkömmlich intellektueller Interpretation nicht im Widerspruch zur damaligen Theologie steht, das man
aber gleichzeitig aus der Sicht der von ihm ebenfalls beschriebenen Meditationsform "Abgeschiedenheit des Geistes" interpretieren kann. Die Abgeschiedenheit des Geistes
entspricht im tantrischen Buddhismus weitestgehend der Mahamudra-Meditation
sowie dem Maha-Ati, bei denen der oben beschriebene Symmetriebruch zwischen den Phasen
im Nachgang erkannt werden kann.
In den deutschen Übersetzungen werden dieser und auch andere Texte Meister Eckharts vom herkömmlichen Intellekt mit seinen konzeptuellen Erwägungen interpretiert.
Da nur wenigen Menschen die von Chögyam Trungpa und Herbert Guenther beschriebene Sichtweise eines andersartigen Denkens auf Basis einer selbst-existierenden Intelligenz
zugänglich wird, kann man davon ausgehen, dass die
Doppeldeutigkeit der Ausführungen Meister Eckharts damals ebenfalls unerkannt geblieben ist. Beispielsweise:
"UBI NOTA QUOD UNITAS SIVE UNUM VIDETUR PROPRIUM ET PROPRIETAS INTELLECTUS SOLIUS."
wird beispielsweise von Dietmar Mieth (2002) übersetzt und ist identisch mit der von Joseph Koch et al. vorher entstandenen Übersetzung, die im Auftrag der Deutschen Forschungsgemeinschaft (1956-1987) entstand:
Hierzu bemerke, daß die Einheit oder das Eine das Eigentümliche und die Eigentümlichkeit des Intellekts allein zu sein scheint
Weiter heißt es (mit Übersetzung von Joseph Koch):
... DEUS VIDENS, DEUS VIDENTIUM, QUI SILICET INTELLEGIT ET SOLO INTELLECTU CAPITUR QUI EST INTELLECTUS SE TOTO.
"... der schauende Gott, der Gott der Schauenden, das heißt, der denkt und mit dem Intellekt allein erfaßt wird, der ganz und gar Intellekt ist."
Für diejenigen, die Erfahrungen mit Mahamudra-Meditation bzw. Meister Eckharts Form der Abgeschiedenheit des Geistes haben,
bleibt diese hier verbal wiedergegebene Auffassung unzureichend. Das liegt auch daran, dass das Wort "INTELLECTUS" verwendet wurde,
das im Deutschen mehrere Wortbedeutungen umfasst und im Laufe
der Jahrhunderte auch mehrfach seinen Wortsinn veränderte.
Für die Sichtweise aus dem Mahamudra oder Maha-Ati gibt es im Deutschen allerdings keinen befriedigenden Ausdruck. Den dafür im
Tibetischen bestehenden Ausdruck "sems-nyid", der danach auch die Sichtweise Meister Eckharts wiedergeben sollte, übersetzt Herbert Guenther aus den Texten
Padmasambhavas beispielsweise mit "Denken des Denkens (des Seins); Denken an sich; reine Intensität des Denkens; das, was die geistige Substanz zu einer geistigen Substanz macht, geistige
Anlagen; das was die Psyche zu dem macht, was sie ist; was unsere Mentalität zu einer Mentalität macht". Wenn man diese Bedeutungen anstelle des Begriffs "Intellekt"
hinterlegt, ergibt sich auch ein anderes Verständnis für die von Dietmar Mieth oder Joseph Koch übersetzten Aussagen zu Gott.
In seiner Predigt "BEATI PAUPERES SPIRITU,
QUONIAM IPSORUM EST REGNUM CAELORUM" zeigt Meister Eckhart, dass er Erfahrungen gemacht hat, wie sie auch beim Mahamudra bekannt sind, indem er sagt:
... er [der Mensch] muß vielmehr so ledig sein allen Wissens, daß er nicht wisse, noch erkenne, noch empfinde, daß Gott in ihm lebt; mehr noch; er soll ledig sein allen Erkennens, das in ihm lebendig ist.
Auch geht Meister Eckhart auf die Problematik des Verstehens seiner Aussagen ein, indem er ausdrückt, dass es von ihm Aussagen gibt, die dem herkömmlichen intellektuellen Verständnis (2. und 3. Nen, im Tibetischen sems-blo) entsprechen und andererseits Aussagen, die der Sicht des Denkens als solches (sems-nyid) entsprechen, bei der ausgehend vom 2. und 3. Nen eine Sicht auf den 1. Nen geworfen wird. Er sagt:
Wer diese Rede nicht versteht, der bekümmere sein Herz nicht damit. Denn, solange der Mensch dieser Wahrheit nicht gleicht, solange wird er diese Rede nicht verstehen; denn dies ist eine unverhüllte Wahrheit, die aus dem Herzen Gottes kommt.
Aus dieser Sicht heraus ist auch der folgende Text zu verstehen, der ebenfalls aus Sermon XXIX "DEUS UNUS EST" stammt. Hier ein wörtliches Zitat einer Übersetzung von Dietmar Mieth:
Der Intellekt ist ja im eigentlichen Sinnes Gottes, Gott aber ist einer. Wieviel also an Intellekt oder an Denkvermögen ein jedes hat, so viel hat es von Gott. Denn der eine Gott ist Intellekt, und der Intellekt ist der eine Gott. Daher ist Gott niemals und nirgends Gott außer im Intellekt. ... Zum Intellekt aufsteigen und sich ihm unterwerfen bedeutet also mit Gott vereinigt zu werden. Geeint werden, eines sein, ist eins mit Gott sein. Denn Gott ist einer, alles Sein neben dem Intellekt, außerhalb des Intellekts ist Geschöpf, ist erschaffbar, ist etwas anderes als Gott, ist nicht Gott, denn in Gott gibt es kein Anderes.
Der Vollständigkeit halber hier auch der Auszug aus dem Original-Text:
INTELLECTUS ENIM PROPRIE DEI EST, DEUS AUTEM UNUS. IGITUR QUANTUM HABET UNUMQUODQUE DE INTELLECTU SIVE DE INTELLECTUALI, TANTUM HABET DEI ET TANTUM DE UNO ET TANTUM DE ESSE UNUM CUM DEO. DEUS ENIM UNUS EST INTELLECTUS, ET INTELLECTUS EST DEUS UNUS. UNDE DEUS NUNQUAM ET NUSQUAM EST UT DEUS NISI IN INTELLECTU. ... ASCENDERE IGITUR AD INTELLECTUM, SUBDI IPSI, EST UNIRI DEO. UNIRI, UNUM ESSE, EST CUM DEUM ESSE. DEUS ENIM UNUS EST. OMNE ESSE PRAETER INTELLECTUM, EXTRA INTELLECTUM CREATURA EST, CREABILE EST, ALIUD EST A DEO, DEUS NON EST. IN DEO ENIM NON EST ALIUD.
Gegen diese Übersetzung Dietmar Mieths ist nichts einzuwenden (lediglich ein kleiner Flüchtigkeitsfehler im ersten Satz). Aber mit der weitergehenden Bedeutung des Begriffs "Intellekt" kommt man zu dem Ergebnis, dass Gott in seinem Aspekt als "vom Menschen getrennt" nicht konzeptuell denken kann, keine Bewertungen vornehmen kann und auch nicht einmal erkennen kann, was außerhalb von ihm geschieht. Das ist für das Christentum mit der Grundlage der Bibel und dem dort enthaltenen Dualismus natürlich eine nicht akzeptable, häretische Auslegung. Es gilt dann nicht einmal mehr die Aussage "Am Anfang war das Wort". Zu der Übersetzung des im lateinischen Text benutzten Wortes "LOGOS" sagt Meister Eckhart in seinem Sermon "GRATIA DOMINI NOSTRI JESU CHRISTI":
... Daher heißt es "Am Anfang war das Wort" (Joh 1,1), der LOGOS, wie der Grieche sagt, was Idee heißt.
Durch Meister Eckharts vorgenommene Richtigstellung beim Begriff "LOGOS", der umfangreichen unterschiedlichen Bedeutungen entsprechen kann, mit dem von ihm gewählten
Begriff "Idee" ergibt sich ein neuer Sinn. Während der Begriff "Wort" mit konzeptuellem Denken verbunden ist, kann "Idee" hiervon frei sein und sich auf
Spontaneität oder einen Impuls beziehen, was beim Begriff "Wort" nicht der Fall ist. "Wort" bezieht sich auf den 2. und 3. Nen, während "Idee" eine Verknüpfung zum
1. Nen zulässt. Damit legt Meister Eckhart diesen Bibelspruch ganz anders aus; er zeigt, dass eine nonverbale Idee spontan geboren wird - ähnlich wie eine
Vakuumfluktuation - , während verbale Gedanken erst nachfolgend greifen.
Genau das entspricht den Messungen beim Libet-Experiment. Entscheidungen
können entstehen, bevor das menschliche Bewusstsein oder der Intellekt aktiv werden. Das passt auch mit der vorherigen Deutung zu "INTELLECTUS" zusammen, dass Gott nicht
konzeptuell denken kann, aber durch nonverbal getroffene Entscheidungen (1. Nen) wirken kann.
Einige Zeilen weiter zeigt sich, dass das buddhistische Prinzip der 3 Kayas starke Gemeinsamkeiten mit der Trinität aufweist. Meister Eckhart führt aus:
Der Vater ist der, aus dem alles der Wirkung nach, der Sohn der, durch den alles der Form nach, der Heilige Geist der, in dem alles dem Ziel nach ist. ...
Nicht gehört Gott zu allen Dingen, sondern er ist die Ursache und der Grund aller Dinge und er ist über allen und hat nicht teil an ihrer Zählung, Teilung oder Unterscheidung. Bemerke hierzu, daß das aus ihm nicht die Wirk-Ursache, sondern die Idee der Wirk-Ursache ist. Ähnlich ist das durch ihn die Idee der Form-Ursache und das in ihm der LOGOS oder die Idee der Ziel-Ursache.
Dieses Prinzip findet sich auch in dem Systementwurf Ralf Ottes mit seinen Möglichkeitsfeldern und den virtuellen Beobachtungsfeldern wieder, die mittels einer
hyperkomplexen Algebra durch eine Übertragungsfunktion verknüpft und gespiegelt werden. Hierin spiegelt sich auch das Prinzip der Drei Nen des Zen-Meisters Katsuki Sekida.
Erst die (evolutionäre) Entwicklung des geistigen Vermögens wie beim Menschen hat es erlaubt,
konzeptuelles Denken, Bewertungen usw. (2. und 3. Nen) vorzunehmen. Erst in dieser vollständigen Einheit Gottes mit einem konzeptuellen Verstand
ist diese konzeptuelle Form des Denkens möglich; diese Einheit wird im tibetischen Buddhismus Svabhavikakaya genannt, der allerdings nontheistisch zu sehen ist.
Mit seinen Aussagen nähert sich Meister Eckhart
vorsichtig, aber nicht vollständig der Philosophie eines Panentheismus an. Hätten seine Inquisitoren diese Doppelbedeutung seiner Aussagen verstanden,
wäre Meister Eckhart vermutlich ebenfalls auf
dem Scheiterhaufen gelandet.
Wenn man vom Kreationismus und der dualistischen Trennung zwischen dem Erschaffenden (Gott) und dem Erschafften innerhalb der Aussagen Meister Eckhards absieht,
dann kommt er auch dem Pantheismus sowie der monistischen buddhistischen
Philosophie des Cittamatra der Yogacarins auf Basis des Lankavatara-Sutra nahe, die auf der absoluten Ebene das "EINE ALLUMFASSENDE BEWUSSTSEIN"
(tib. citta) in einer Nur-Geist-Lehre ansehen (, die sich allerdings in einigen
Aussagen von der Philosophie Nagarjunas, dem Madhyamaka, und dem Dzogchen unterscheidet). In all diesen und auch anderen Anschauungen stößt man
dann auf die Frage, wie es zum Denken an sich, dem sems-nyid im 1. Nen kommt. Als nicht-theistische Antwort könnte man als Basis den von Ralf Otte definierten Raum aller
Möglichkeiten ansehen, der durch Schwarmregeln in Verbindung mit Wahrscheinlichkeiten zu den von Chögyam Trungpa und Padmasambhava genannten Formen des Denkens führt.
Die selbst-existierende Intelligenz könnte man dann als eine Form von Schwarmintelligenz ansehen.
Bei diesen Interpretationen muss einem aber klar sein,
dass diese auf dem 2. und 3. Nen (sems-blo) beruhen, die ihrerseits auch auf Fehlinterpretationen beruhen können. Derartige Fehlinterpretationen werden
vom subjektiven Ich (virtuelles Beobachtungsfeld bzw. 3. Nen) als Wahrheit aufgefasst, unabhängig davon was andere als Wahrheit ansehen und wie eine absolute Wahrheit
im 1. Nen aussehen könnte. Aus dem Wesen der Drei Nen geht hervor, dass im Bereich des Relativen unbegrenzt viele Wahrheiten/Interpretationen gleichzeitig bestehen können.
Vasilii V. Nalimov hat den Nachweis erbracht, dass Sprache bei ihrer Interpretation nicht
nur zu unbegrenzt vielen Möglichkeiten führt,
sondern dass die Zuweisung von Bedeutungen über eine Bedeutungsentwicklung (Semantik) bei Einzelindividuen und Gruppen über Jahre und Jahrhunderte hinweg auf Basis
von Wahrscheinlichkeiten beruht, die der Bayes'schen Logik unterworfen sind.
V.V. Nalimov zeigt, wie hierdurch auch eine Vieldimensionalität jeder einzelnen Persönlichkeit
entsteht. Der von ihm verwendete mathematische Formalismus ist mit dem in der Quantenmechanik vergleichbar und sollte sich somit auch in den virtuellen
Beobachtungsfeldern von Ralf Otte als Superpositionen imaginärer Werte auffinden lassen.
In menschlichem Verhalten lässt sich vielfach Schwarmverhalten finden (z.B. La Ola-Welle, Straßenverkehr, Wahlen). In Bezug auf die Entdeckungen
von V.V. Nalimov resultiert die Frage, ob Sprachsyntax als Schwarmregeln angesehen werden kann und ob Semantik auf Basis dieser Regeln einer Menge von Bedeutungen
entspricht, wobei die durch die Bayes'sche Logik sich ergebenden Wahrscheinlichkeitswerte zur einer jeweils aktuellen Situation eine Bedeutung
selektieren; das Ergebnis wäre dann das aktuelle Sprechgeschehen. Das Sprechgeschehen entspricht seinerseits verbalisierten Gedanken, so dass
sich hier auch ein Modell für Denkprozesse auf Basis von Schwarmregeln in Verbindung mit Wahrscheinlichkeitswerten ergeben sollte. Nach V.V. Nalimov
ergibt sich durch die Vision einer Welt, die auf Semantik und auf Wahrscheinlichkeiten mit Regeln der Bayes'schen Logik und einem Zufallsprinzip
beruht, die Konsequenz, dass ein freier Wille nicht existiert. Ein freier Wille mit einem Bezug auf Ursache und Wirkung kann allenfalls als unscharf in
Analogie zur Quantenmechanik charakterisiert werden. V.V. Nalimov zitiert hierzu Max Born:
[in quantum mechanics] we have the paradoxical situation that observable events obey laws of chance, but that the probability for these events itself spreads according to laws which are in all essential features causal laws.
V.V. Nalimov ergänzt hierzu:
Now if we deal with a quantum ensemble exhaustively described by a set of dynamic variables q1, q2, ..., which are measured simultaneously and independently, the probabilty of finding a definite value of the set is determined by the probability density
WM(q) = |ΨM(q)|2
The wave function WM is explicitly given as a function of the coordinates q. It determines the statistics of any measurement of the microsystem compatible with a macrosystem M which dictates the conditions for the changes in the microsystem (Blokhintsev, 1966). It is possible to speak of a probalistically determined potential for a certain behavior under certain macroconditions even for a single electron. Potentiality may be said to be a probalistically determined limit of freedom given to an electron.
Dies entspricht auch den Aussagen Ralf Ottes, wonach eine Wellenfunktion statistisch über Verschränkungskorrelationen auf ein Möglichkeitsfeld einwirken kann
und deren Wahrscheinlichkeitsamplituden verändern kann, wodurch geistige Zustände auf materielle Strukturen einwirken können. Aus buddhistischen Philosophien
wie beispielsweise Nagarjunas Madhyamaka ergibt sich die Folgerung, dass materielle Strukturen aber lediglich dem Anschein nach bestehen; auch einige Interpretationen der
Quantenphysik kommen zu diesem Ergebnis, wonach die materiellen Strukturen aus dem virtuellen Beobachtungsfeld geistig gespiegelte Formationen wären.
Unklar bleibt aber weiterhin, wie aus einer einzelnen Wellenfunktion ein Schwarm mit vielen "Teilnehmern" und "Nachbarschaftsbeziehungen" gebildet werden kann.
Zu untersuchen wäre, ob über die Einwirkung von Störgrößen aus dem virtuellen Beobachtungsfeld eine Amplitudenmodulation der Wellenfunktion im Möglichkeitsfeld
erzielt werden kann. Denkbar wäre dann, dass dies zu Überlagerungszuständen bezogen auf die Julia-Fläche führt. Die gleichzeitig vorhandenen Überlagerungen
könnte man dann als Schwarm ansehen, dessen Schwarmmitglieder über Kohärenz als "Nachbarn" gelten könnten. Durch das oben beschriebene Auswahlverfahren würde dann
bei einer hinreichend starken Impulsstärke mittels der Übertragungsfunktion (Spiegelung) eine Beobachtung im virtuellen Beobachtungsfeld als Folge einer
Dekohärenz möglich. Dieser denkbare
Prozess befände sich wiederum in Übereinstimmung mit dem Ablauf der Drei Nen. Katsuki Sekida beschreibt außerdem die Situation, dass bei unzureichender Impulsstärke des
1. Nen dieser 1. Nen vorübergehend oder dauernd in einer Art Ruhezustand verborgen bleiben kann (beispielsweise als verdrängte Erinnerungen in einem
"Ozean" von Erinnerungen). Verborgene 1. Nen
können aber durch bestimmte Bedingungen beim 2. oder 3. Nen (beispielsweise durch Psychotherapie) durch eine Art Resonanz ausgehend vom
virtuellen Beobachtungsfeld auf eine höhere Impulsstärke gebracht werden, so dass ein derartiger 1. Nen sich wieder in die
rekursive Baumstruktur der Drei Nen eingliedert
und dann vom 2. und 3. Nen wieder erkannt werden können - ebenfalls in Übereinstimmung mit dem oben genannten Selektionsprozess. Die verborgenen 1. Nen könnten
ihrerseits möglicherweise ebenfalls als Schwarm angesehen werden. Derartige Überlegungen bedürfen aber einer tiefer gehenden Prüfung; ebenso die
Suche nach weiteren Alternativen für Schwarmprozesse innerhalb der Möglichkeitsfelder.
Im Hinblick auf Sprache lässt sich dann hier auch als Konsequenz ableiten, dass der Begriff "Gott" oder auch andere Sachverhalte des Absoluten sich nicht durch Sprache
semantisch ausreichend abbilden lassen. Sprache kann
hier allenfalls einen Hinweis darauf geben, wie man sich dem Absoluten geistig annähern kann und wie man beispielsweise durch Meditation Absolutes erleben kann.
Sprache entspricht damit nur einem Wegweiser; den Weg gehen, muss dann jede/r selbst, um zu einem entsprechenden Erleben zu gelangen.
Bezogen auf die Libet-Experimente und die Frage nach der Entscheidungsfreiheit gibt es einen weiteren deutlichen Hinweis von Chögyam Trungpa, wobei er
auf den Dharmakaya Bezug nimmt, den man stellvertretend für Ralf Ottes Möglichkeitsfelder ansehen kann. Zitat:
Der Dharmakaya ist durch nichts bedingt. Der Sprung wurde schon gemacht. Wenn wir uns eindeutig dafür entscheiden zu springen, sind wir schon gesprungen. Das Springen selbst ist wie eine Wiederholung oder etwas Überflüssiges. Wenn wir uns einmal entschieden haben zu springen, sind wir bereits gesprungen.
Im Dzogchen bleibt eine Polarität von Entscheidungsfreiheit und Determinismus ohne Bedeutung. James Low sagt hierzu, dass Handlungen aus der Spontaneität des
non-dualen Feldes entstehen.
Um sich den Denkprozessen als solchen (sems-nyid) im Dharmakaya bzw. in den Möglichkeitsfeldern besser annähern zu können, kann man versuchen,
das Thema der 1. Nen von Katsuki Sekida in Anlehnung
an die Möglichkeitsfelder mit dem Beispiel von Julia-Funktionen weiter zu betrachten.
Aus Katsuki Sekidas Modell lässt sich für den Zustand des Samadhi eine Kette der 1. Nen ableiten,
die modellhaft dem Denkprozess an sich (sems-nyid) ohne die konzeptuellen Gedanken
des 2. und 3. Nen (sems-blo) entspricht. Dies entspräche dann dem von Meister Eckhart beschriebenen Denkprozess Gottes in seinem Aspekt einer Getrenntheit vom Menschen;
dieser Denkprozess ließe dann auf
absoluter Ebene (1. Nen) bei Auswahl von Alternativen/Möglichkeiten auf Basis ihrer Wahrscheinlichkeitswerte durch eine Schwarmintelligenz und auch
auf Basis von Zufall das Treffen von Entscheidungen zu, ohne dass konzeptuelle Gedanken, Bewertungen, usw. berücksichtigt würden.
Diese Kette der 1. Nen lässt sich durch die folgende Grafik veranschaulichen:
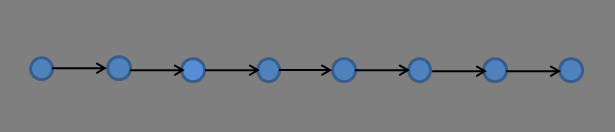
Vielleicht lässt sich für diese einfacheren Gedankenketten leichter ein Abbild im Modell von Ralf Otte finden. Allerdings bleibt bei der Kette der 1. Nen offen,
was innerhalb einer jeden Phase der Gedankenkette passiert. Die Kette der 1. Nen erscheint aber ähnlich wie die Startsequenzen einzelner Trajektorien, die
zur Ausbildung von Attraktoren innerhalb von Julia-Mengen führen. Vergleiche hierzu die Bilder 1-3 aus Serie 1 oben.
Bild 1 (Serie 4) zeigt den Startpunkt (weiß) und den Endpunkt (rot) einer Iteration einer Julia-Funktion mit stärker strukturierten Flächen.
Bei den Bildern 2-4 wurde als neue Störgröße c der Wert der 50. Iteration von Bild 1 angesetzt (ci+1=ci) und daran
anschließend erneut 50 Iterationen ausgeführt.
Es zeigt sich eine selbst gesteuerte Konsolidierung der Trajektorie, die gleichzeitig mit einer Harmonisierung der Julia-Fläche einhergeht, bei der
sowohl die Verästelungen in der Struktur reduziert werden als auch die Wahrscheinlichkeitsdichten erhöht werden. Erkennbar ist dies
an der einfacheren Struktur der Trajektorie und am Unterschied
der Farbgebung innerhalb der teilweise rot gefärbten Julia-Fläche in Bild 1 gegenüber einer einheitlicheren, dunkleren Färbung in den Bildern 2-4.
Die Bilder 2-4 zeigen außerdem alternierende Endpunkte der Trajektorie, die von Ralf Otte als alternierende Wahrnehmungen gedeutet werden.
In Bild 5 wird der Beginn der Trajektorie nach der 3. Iteration gezeigt. Nach Anagarika Govinda beginnt erst nach
der 5. Schwingung die bewusst werdende Wahrnehmungsphase mit dem 2. und 3. Nen, während Wahrnehmungsvorgänge bei der 3. und 4. Schwingung noch unbewusst bleiben; dies
lässt sich auch mit den oben erwähnten Untersuchungsergebnissen von David J. Freedman über Wahrnehmungen und Entscheidungen im Stammhirn vereinbaren.
Hieraus folgt allerdings auch, dass speziell die Kette der 1. Nen immer nur aus wenigen Iterationsschritten bestehen kann, wobei kein
2. oder 3. Nen erzeugt wird. In Anhang I "Spontaneität versus Impulsivität" wird gezeigt,
wie es zum Abbruch/Kollaps von Iterationen kommen kann, aus denen anschließend wieder eine neue Gedankenkette beginnend mit einem
neuen 1. Nen hervorgeht.
In Bild 6 wird für die 4. Iteration der aus der 3. Iteration berechnete Endzustand der Trajektorie als neue Störgröße verwendet.
Dieser Prozess für c mit (ci+1=ci) müsste eigentlich auch bei der Berechnung des Attraktors wie bei Bild 1 mit 50 Iterationen durchgeführt werden, um den
Konsolidierungsprozess genauer verfolgen zu können. Ob die Resultate dabei signifikant von der Trajektorie aus Bild 1 abweichen, wurde hier
(noch) nicht untersucht. Das divergierende, sich selbst organisierende Verhalten des Attraktors zeigt sich in den Bildern 7 und 8. Während eine direkte 16-fache Iteration bei Bild 7
mit unveränderlicher Störgröße c ein stabiles Ergebnis des Attraktors innerhalb der Julia-Fläche erzeugt, wird nach einer Übernahme der Störgröße c wie bei Bild 4 bei ebenfalls
16-facher Iteration ein repulsives Verhalten erzeugt. Das Auftreten eines repulsiven Endpunkts bei der 16. Iteration (bzw. hier bereits ab der 8. Iteration)
würde nach dem Modell von Lama Anagarika Govinda bedeuten,
dass eine Wahrnehmung erkannt und reflexiv-bewusst geworden ist, dass diese Wahrnehmung aber nicht zu einer vollständig selbst-reflexiven Empfindung geführt hat. Das wäre
beispielsweise vergleichbar mit der Wahrnehmung eines Säugetieres.
Bisher nicht durchgeführt wurde eine Untersuchung, welche Ergebnisse im Regelfall entstehen, wenn man immer bei jedem
Iterationsschritt c auf (ci+1 := ci) setzt, was bei einem sich selbst-organisierenden System denkbar wäre.
Generell muss aber gesagt werden, dass nicht klar ist, ob die Zahl der Schwingungen mit der Zahl der Iterationen übereinstimmt.
Hier sind noch viele ungeklärte Annahmen im Spiel. Auch das Verhältnis zwischen den einzelnen Phasen in der Kette des 1. Nen und der Anzahl von Schwingungen ist ungeklärt
wie auch die Auswirkungen auf das Iterierte Funktionensystem bei einem Wechsel von einem 1. Nen zum nächsten 1. Nen. Auch wie Schwarmregeln aussehen könnten, die der
selbst-existierenden Intelligenz entsprechen, ist bisher vollkommen unbekannt und nach buddhistischer Auffassung auch nicht bestimmbar.
Im folgenden Abschnitt wird dargestellt, wie sich der Prozess der Bewusstwerdung durch Rückspiegelungen als Schwarmprozess
simulieren lässt.